计组部分试卷&重点题目分析

一些试卷的解析

20-21 HY B

Note

解析

采用 8 位带符号补码计算 (-111)+(-34)。

先将 -111 转换为补码。111 的二进制为 0110 1111，按补码规则取反加一得到 1001 0001，因此 -111 的 8 位补码是 1001 0001。

再将 -34 转换为补码。34 的二进制为 0010 0010，取反加一得到 1101 1110，因此 -34 的 8 位补码是 1101 1110。

进行补码加法：1001 0001 + 1101 1110 = 1 0110 1111，丢弃最高位进位后结果为 0110 1111。

判断溢出。两个加数符号位均为 1，结果符号位为 0，负数加负数却得到正数，发生溢出。

因此运算结果为 0110 1111，且有溢出，正确选项为 A。

Note

解析 0x10-0x24=-0x14=-20，然后由于b型指令的偏移计算是imm*2，所以填入的立即数是-10，换算为十六进制应该是0xFF6

Note

解析 jr 指令的语义是无条件跳转到寄存器中给出的地址。RISC-V 中没有 jr，但可以用 jalr 指令实现同样功能，因为 jalr 以寄存器加立即数作为跳转目标地址。正确选项为 B。

Tip

reg一般代表寄存器，于是和寄存器有关的缩写大多带有r，可以凭借这个进行判断

Note

解析 循环中分支行为为连续 9 次跳转，随后 1 次不跳转，模式周期为 10。

1 位预测器在第一次状态稳定后，每遇到最后一次不跳转会预测错误一次，因此 10 次中错 1 次，准确率为 9/10 = 90%，但首次进入循环还会多错一次，长期平均为 8/10≈ 80%。

2 位预测器在稳定后，仅在状态翻转时错一次，每个周期只在那一次不跳转时错，10 次中错 1 次，准确率为 9/10 = 90%，对应选项为 B。

Tip

相关考点 以本题的循环为背景，分支行为模式可以抽象为：连续 9 次跳转，接着 1 次不跳转，然后再次重复这一过程。 对于 1 位预测器，它只保存“上一次是否跳转”的结果。循环开始后，前 9 次分支都会是跳转，只要预测器进入“预测跳转”状态，就能一直预测正确。到第 10 次分支，实际结果是不跳转，但预测器仍然预测跳转，因此发生一次错误，同时预测器状态被改成“预测不跳转”。接下来重新进入循环时，第 1 次分支的真实结果又是跳转，但预测器仍然预测不跳转，于是再次预测错误，然后状态切回“预测跳转”。因此在一个完整循环周期内，1 位预测器通常会在循环结束和下一次循环开始各错一次。

对于 2 位预测器，它通常用一个 2 位饱和计数器表示状态，比如强跳转、弱跳转、弱不跳转、强不跳转。只要处在“强跳转”或“弱跳转”状态，预测结果都是跳转。循环执行过程中，连续 9 次跳转会把预测器推到“强跳转”状态。到循环结束时出现一次不跳转，预测仍然是跳转，于是发生一次错误，但状态只会从“强跳转”退到“弱跳转”，预测方向并不会立刻翻转。下一次重新进入循环时，真实结果又是跳转，预测器仍预测跳转，因此不再出错，并很快回到“强跳转”状态。这样在每个循环周期内，2 位预测器只会在那一次不跳转时出错一次。

Note

解析 在单周期 CPU 中，所有指令都必须在一个时钟周期内完成，所以时钟周期要足够长以覆盖“最慢指令”的组合逻辑延迟，时钟频率就由最慢指令决定。四个选项里通常最慢的是访存指令，且 load 一般比 store 更慢，因为 load 需要从存储器读出数据并回写寄存器，而 store 不需要回写寄存器，路径更短。因此由 ld 的执行时间决定。答案选 A。

Note

解析 这是一条典型的无前递、无冒险检测的 5 级流水数据相关插入 NOP 问题。关键规则是寄存器在同一周期前半写、后半读，所以只要消费者指令的读寄存器阶段 ID 与生产者指令的写回阶段 WB 落在同一周期也可以读到新值；否则就必须把消费者的 ID 推迟到不早于生产者的 WB。

先看相关链：x11 由第一条 addi 写回，x12 由第二条 ld 写回，第三条 add 同时读 x11 和 x12，所以它的 ID 必须不早于第二条 ld 的 WB。按正常不插空的时序，第三条 add 的 ID 会比 ld 的 WB 早两拍，因此至少要在 ld 与 add 之间插入 2 条 NOP，才能把 add 的 ID 推到与 ld 的 WB 同周期，从而在后半周期读到 x12，同时 x11 也早已写回满足。

再看第五条 add 读 x13，而 x13 由第三条 add 写回。即使前面已经插了 2 条 NOP，第五条 add 的 ID 仍会比第三条 add 的 WB 早一拍，因此还需要在第四条与第五条之间再插入 1 条 NOP，把第五条 add 的 ID 推迟到与第三条 add 的 WB 同周期后半读到 x13。

因此最少需要插入 3 条 NOP，对应选项 B。

Note

解析 第七题：C

• A:分支判定点更靠后、误预测清空的指令更多，因此这是成立
• B:典型例子就是 load-use 冒险，数据要到 MEM/WB 才产生，旁路也来不及，这是标准结论，正确。
• C:同B的解释
• D:静态调度可以减少数据冒险和控制冒险带来的停顿。

第八题：D

• A:增加一级 cache 大小不一定降低不命中率，受工作集和访问特性影响
• B:直达没有被淘汰
• C:多级Cache通常采用不同的数据块大小
• D:笔记中的典型例子，计算机更希望你的算法可以一行行查找而不是一列列查找

Note

解析 平均读时间约等于平均寻道时间加平均旋转等待时间加数据传输时间。

7200RPM 表示每分钟 7200 转，每秒 7200/60=120 转，所以一圈周期为 1/120 秒=0.008333 秒=8.333ms，平均旋转等待时间**取半圈为 4.167ms。**平均寻道时间**给定为 8ms。传输 512B，速率 4MB/s=4×1024×1024 B/s=4194304B/s，所以**传输时间**为 512/4194304 秒=0.000122 秒=0.122ms。**总时间**约为 8 + 4.167 + 0.122 = 12.289ms，约等于 12.29ms，**对应选项 B。

Tip

单位中遇到的 P/p 一般都是 per 的缩写，即 每**的意思；遇到的 M/m 有可能是 min 的缩写，也就是分钟；也有 C/c 有可能是 cycle 的缩写，即**周期；I 大概率为 instruction 的缩写，也就是**指令**。CPI=n 的意思是：n 个时钟周期每指令，即每条指令花费的时钟周期

Note

解析 先算 Cache 中用于存数据的位数。能存放 4K 字数据，1 字为 32 位，因此数据区大小为 4096×32=131072 位，即 128K 位。

主存按字节编址，主存块大小为 4 字，每字 32 位，也就是 16 字节，所以 块内偏移**需要 log₂16=4 位。Cache 为直接映射，块数等于主存块数，Cache 中共有 4096/4=1024 行，因此**索引位数**为 log₂1024=10 位。主存地址为 32 位，所以**标记位数 为 32-10-4=18 位。

采用写回策略，每个 Cache 行还需要 1 个有效位和 1 个修改位，因此每行的控制信息位数为 18+1+1=20 位。控制信息总位数为 1024×20=20480 位，约为 20K 位。

将数据区和控制信息相加，总容量为 128K+20K=148K 位。因此答案为 C。

Tip

Cache的计算主要是理解Cache都装了些什么。简单来说，Cache里面有两部分：数据内容，控制内容。

数据内容是神圣而不可侵犯的，说啥就是啥，并且题目一般给你的 存放4K字数据 这种就是描述的这一部分的容量。

一般考察点就在控制内容的长度上。

控制内容的计算我们不从Cache入手，而是从主存那边入手。

主存地址为32/64位，就说明它这里有32/64位的容量，其中应该包括的有：主存块的地址、主存块里面的具体地址、标记

举个例子：有一片住宅区（整个主存），我们先找x单元（某主存块地址），然后找x楼x户（主存块里面的具体地址），然后找这一户里面身份证号是xxx的人（标记）。然后我们的手上只有一串32/64位的数字，前面的x单元、x楼x户的占的位数都是固定的，那么减一下就知道这人身份证号几位了

主存块大小4个字，每个字32位，那每个主存块有128位，也就是16字节。我们按照字节进行编址，那么主存块里的具体地址就应该是0~15，也就是占4位——这是主存块里面的具体地址

接下来算主存块地址需要几位，Cache能放4K字数据，然后每个内存块有4字 => 有1K个内存块，也就是需要10位来表示内存块的地址。

那么我们可以算出来“身份证号”位数为 \(32-10-4=18\) 位——标记位 18 位

然后就是一些需要记得内容：回写法直接映射需要一个修改位和一个有效位，所以控制内容的总位数是 标记位18位+修改位1位+有效位1位=20位

再与数据内容合并，就可以算出来总容量了

Note

解析 已知主频 1GHz，也就是每秒 10^9 个时钟周期，执行周期数 = 执行时间 × 10^9，CPI = 执行周期数 / 动态指令数。

(1) 编译器 A：\(周期数 = 1.1 × 10^9\)，\(指令数 = 1.1 × 10^9\)，所以 \(CPI_A = (1.1×10^9)/(1.1×10^9)=1.0\)。编译器 B：\(周期数 = 1.5 × 10^9\)，\(指令数 = 1.2 × 10^9\)，所以 \(CPI_B = (1.5×10^9)/(1.2×10^9)=1.25\)。

(2) 新编译器：指令数 \(8×10^8，CPI 1.2\)，所以\(周期数 = 8×10^8×1.2=9.6×10^8\)，\(对应时间 = 9.6×10^8 / 10^9 = 0.96 秒\)。相对 A 的加速比 = \(1.1 / 0.96 = 55/48 ≈ 1.146\)。相对 B 的加速比 = \(1.5 / 0.96 = 25/16 = 1.5625\)。

Tip

这种题翻译成中文就行了，下面做个“人话”替换

1GHz => 每秒钟有 \(1\times 10^9\) 个时钟周期；平均CPI => 问你平均每条指令需要几个时钟周期

然后本题告诉你了，1秒钟有多少个时钟周期，又告诉你了运行x条指令对应y秒，那么就很轻松可以计算了

第二问是告诉了你，平均一条指令需要多少时钟周期，又告诉你有多少条指令，同样可以轻松计算了

Note

解析 先从“寄存器含义”开始反推。按照 RISC-V 调用约定，x10 是第 1 个参数，x11 是第 2 个参数，所以函数形参一定是 funct(int x, 另一个参数 y)。再看循环里每次对“当前地址”做 addi x6, x6, 8，说明 y 指向的元素步长是 8 字节，也就是 long long（或 64 位整数），因此 (1) 应是long long int *，形参为 long long int *y。

接着看前两句 slli x5, x10, 3 与 add x5, x5, x11。

x10 是 x，左移 3 位等价于 \(x×8\)；再加上 x11（也就是 y 的起始地址）得到一个“结束地址” \(y + 8x\)。后面紧跟 bge x6, x5, Exit，用的是“当前地址 x6”与“结束地址 x5”比较，满足 x6 >= x5 就退出。因此循环条件本质是“当前指针还没到 y+8x”，等价于按下标写法 i < x，所以 (4) 是 x。

再看 x6 的初值 add x6, x0, x11

把 x11 复制到 x6，说明循环从 y 的起始地址开始访问，也就是 i 从 0 开始；同时题目 C 代码 for 里写的是 int i = (3)，所以 (3) 应为 0。

再看计数变量。

add x8, x0, x0 把 x8 清零，后面在循环中出现 addi x8, x8, 1 表示每次满足某条件就自增一次，因此 C 里 int t = (2) 应为 0，并且 (6) 对应t++，最后 Exit 处 add x10, x8, x0 把 x8 放到返回寄存器 x10，说明 return (8) 是 t。

关键分支条件来自这三句 ld x7, 0(x6) 与 blt x7, x0, Exit 与 addi x8, x8, 1。ld 读出当前元素到 x7，blt x7, x0, Exit 表示“若当前元素 < 0 就退出循环”，退出循环等价于 break；如果没有退出，就执行 t++。因此高层逻辑是 if(当前元素 >= 0) t++ else break。题干里 if 的空是 (5)，所以 (5) 填 y[i] >= 0；对应的 else 语句空 (7) 填 break。

最后解释 i++ 为什么成立。虽然汇编里没有显式的 i 寄存器，但每次 addi x6, x6, 8 都把访问地址推进一个元素，等价于下标 i++ 并访问 y[i]，因此 for 的第三部分 i++ 与汇编中的指针递增是同一件事。 所以完整填空结论是：(1) long long int *，(2) 0，(3) 0，(4) x，(5) y[i] >= 0，(6) t++，(7) break，(8) t

Note

解析

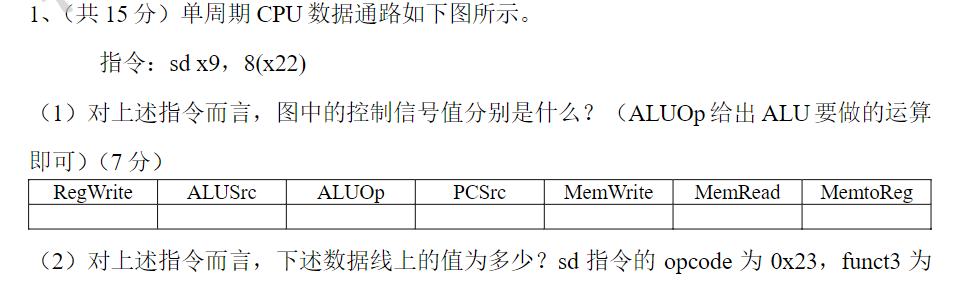
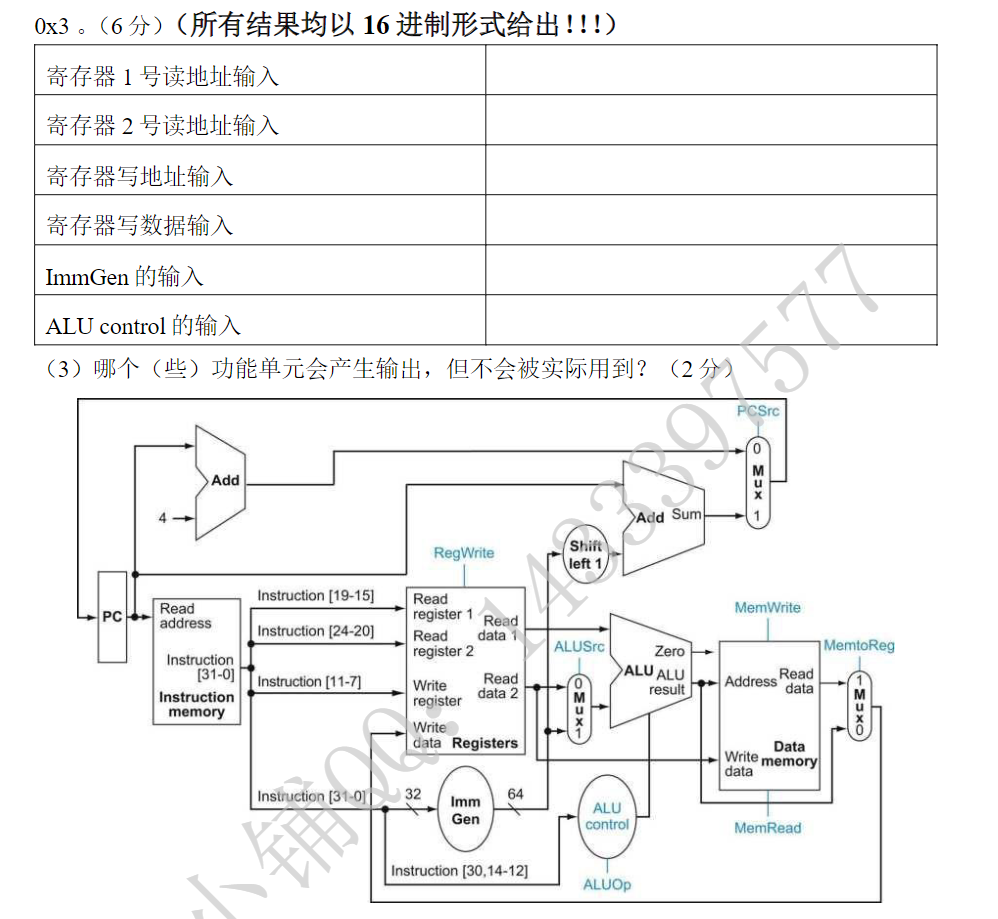
1、把两个数用规格化科学计数法二进制表示：\(12.75_{10}=1100.11_2=1.10011×2^3\)；\(6.5_{10}=110.1_2=1.101×2^2\) 2、对阶： \(1.101×2_2=0.1101×2^3\) 3、尾数相加： \(1.10011+0.1101=10.01101\) 4、结果规格化，并检查溢出和舍入：\(10.01101×2^3=1.001101×2^4\)，没有溢出，无须舍入 5、阶码移码：\(4+15=19\)（\(10011_2\)），正数符号位：\(0\)，尾数 \(001101\)，隐藏 \(1\) 6、二进制位模式和十六进制数：\(0 10011 0011 0100 00\)；\(0X 4CD0\)

Note

解析

1）这题会的话直接背，不会的话看图与推理。

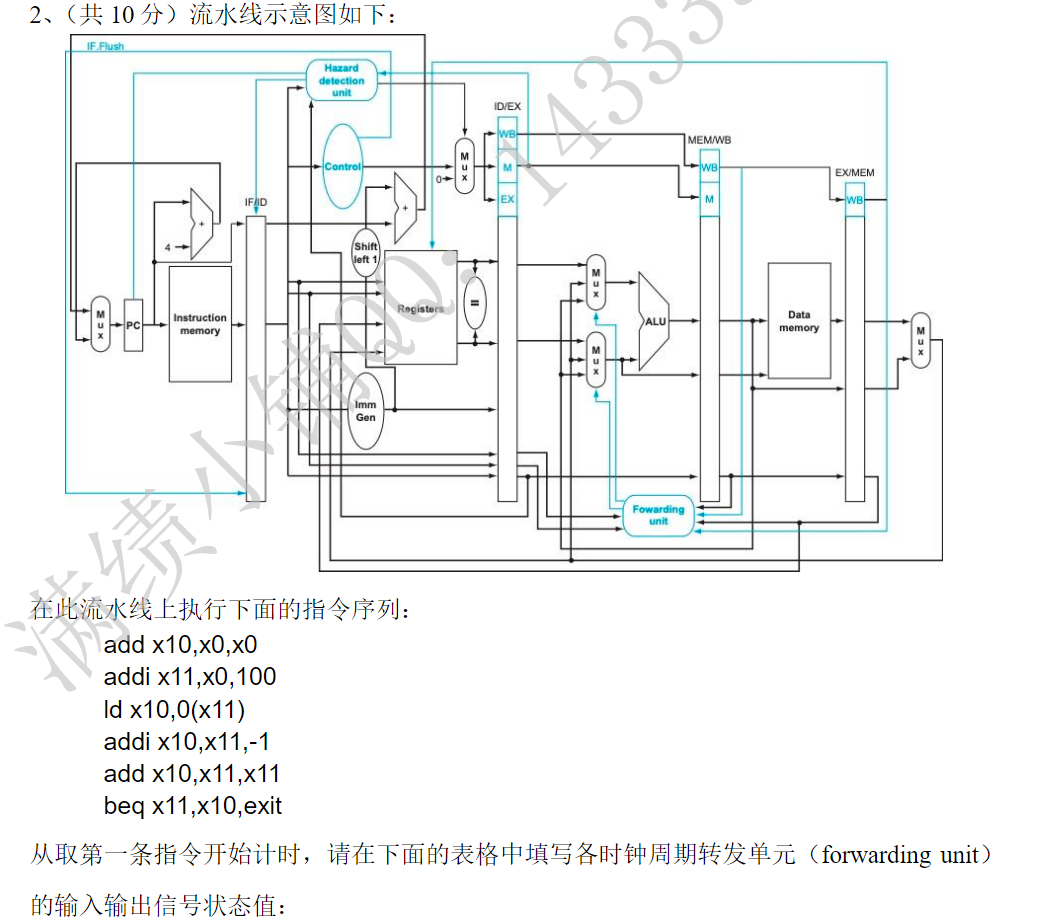
sd x9, 8(x22)是存储指令，表示将寄存器x9中的值存入地址为 x22+8 的位置

-RegWrite： sd指令不涉及寄存器的写入，为0 -ALUSrc：sd指令的源操作数来自寄存器 x22 和常数8，所以ALUSrc为1 - 看图中ALUSrc的部分，是一个多路选择器，当有ImmGen输入的时候就有1，所以为1 -ALUOp：内存访问指令，需要计算地址，所以ALUOp应该设置为进行加法运算，即 00（答案还给了add，估计为了捞捞） -PCSrc：本指令不涉及跳转，所以为0 -MemWrite：本指令为写内存的操作，所以为1 -MemRead：本指令和内存读无关，所以为0 -MemtoReg：未涉及数据写回寄存器，所以为0（答案给的don’t care，神了）

Note

解析

2）这题用到了卷子上面的那个东西

推理一下，题目给了funct3，那么肯定在上面四个选一个，然后我们这里涉及了两个寄存器，所以排除第二个；又涉及了立即数imm，所以排除第一个，接下来就是二选一,既然没复习到那就看运气了，得之我幸，失之我命
这里是S指令，SB型指令其实指的是B型指令
>我们的立即数为8，对应成12位应该是：`0000 0000 1000`，按照S的方法进行拆分，得到了`0000 000`和`01000`
>然后rs2是x9,对应成5位也就是`0 1001`；rs1是x22，对应成5位也就是`1011 0`
>再然后funct3对应`011`，opcode对应`0x23=1011 1`
>组装：`0000 000; 0 1001; 1011 0; 011; 0100; 1011 1`，再按照图上的要求，将内容进行重排即可

Note

解析

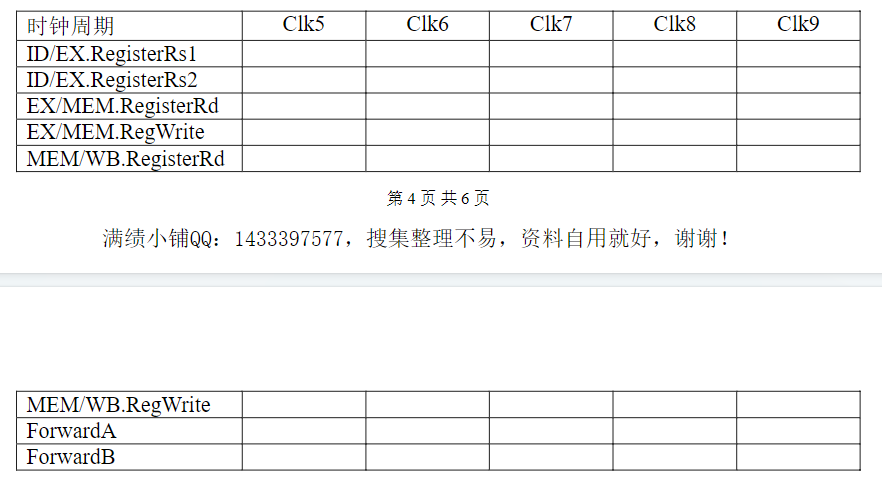
3）第一问的分析中，我们了解到PCSrc等组件是不工作的，那么根据这些组件倒推，看看流程中哪些组件工作了就可以了

PCSrc不工作，但是它之前的Add是工作了的，所以可以说Add为本题答案

我院课本未出现相关知识点，不做解析

Note

解析 已知条件先统一： cache 总大小 4KB，也就是 4096 字节，块大小 64 字节，所以 cache 一共有 4096 / 64 = 64 个块；double 是 8 字节，一个块里能放 64 / 8 = 8 个 double，采用直接映射；cache 初始为空，系统里没有其他程序干扰

代码结构的关键点在于：外层循环跑很多次，但内层每一轮访问数组的方式完全一样。所以性能好坏，取决于“上一轮访问过的数据，下一轮还能不能继续用”

(1) STRIDE = 1，LEN 从 512 变成 1024，为什么性能明显下降

当 LEN = 512，数组大小是 512 × 8 = 4096 字节，正好等于 cache 大小，内层循环第一次完整扫一遍数组时，会把数组对应的 64 个内存块依次放进 cache，由于 cache 正好能装下这 64 个块，它们不会被挤出去，下一次、再下一次外层循环，访问的还是同一批数组元素，这些数据已经在 cache 里，不需要再从内存读，因此除了最开始那一轮比较慢，后面的 1023 轮都很快，整体性能很好**当 LEN = 1024**，数组大小是 1024 × 8 = 8192 字节，是 cache 大小的两倍，内层循环一轮会访问 128 个不同的内存块，cache 只有 64 个块位置，前面装进去的 64 个块，会在后半段访问时被后来的 64 个块替换掉，等下一轮外层循环再次从 array[0] 开始访问时，前半部分的数据已经不在 cache 里了，又要重新从内存读，**结果就是：每一轮内层循环，几乎都要重新读一遍数据**所以，相比 LEN = 512 的情况，慢得多，所以性能明显下降

(2)在第 (1) 问条件下，改成全相联 + LRU，性能会不会提升

不会有本质提升,原因是：问题的根本不在“映射方式”，而在“数据总量太大” ,LEN = 1024 时，一轮需要用到 128 个块，但 cache 只能放 64 个，不管是直接映射还是全相联，都不可能同时保存下一轮还要用到的全部数据，因此每一轮还是要反复从内存加载，性能不会明显改善

(3) STRIDE = 16，LEN = 512 时，cache 利用情况如何；LEN 变成 1024 会发生什么

STRIDE = 16 表示：每次访问 array[j]，下次访问 array[j+16],16 个 double 是 128 字节，相当于每次跨过 2 个块,也就是说，每访问一次，就跳到一个新的块，而且在这个块里只用到 1 个 double LEN = 512 时：内层循环一共访问 512 / 16 = 32 次，对应 32 个不同的块，cache 有 64 个块位置，这 32 个块都能放进去，而且不会互相顶掉，所以从第二轮外层循环开始，这 32 个块都还能直接用，从“块是否被用到”的角度看，只用了 64 个块里的一半，也就是 50%，从“块内部是否被充分用到”的角度看，每个块 8 个 double 只用了 1 个，利用率是 ⅛**LEN = 1024 时**：内层循环访问 1024 / 16 = 64 次，对应 64 个不同的块，数量刚好等于 cache 块数，但由于是直接映射，这 64 个块中有一半会映射到同样的位置，结果是：后访问的块会把先访问的块替换掉，下一轮再访问先前的数据时，又要重新加载，因此程序会频繁地把数据装进 cache、又很快被替换掉，性能明显变差，此时从“块位置占用”来看，仍然主要只用到了其中一半的位置，但每次访问都要重新加载

(4) 在第 (3) 问前提下，改成全相联 + LRU，性能会不会提升

会，而且在 LEN = 1024 时提升非常明显，因为 STRIDE = 16、LEN = 1024 的情况下，一轮内层循环正好访问 64 个不同的块，cache 也正好能放下 64 个块，如果不再强制固定映射位置，这 64 个块就可以同时留在 cache 里，这样第一轮把它们装进去后，后续外层循环都可以直接使用，不再反复从内存加载，所以相比直接映射，执行速度会有明显改善

Note

解析

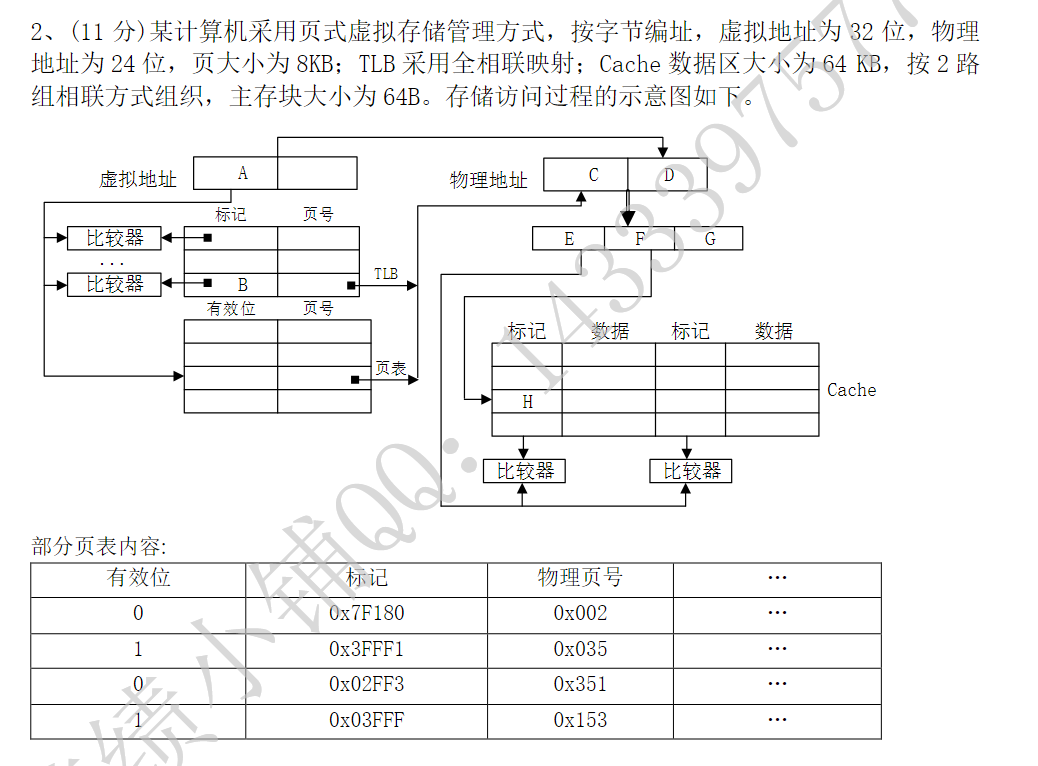
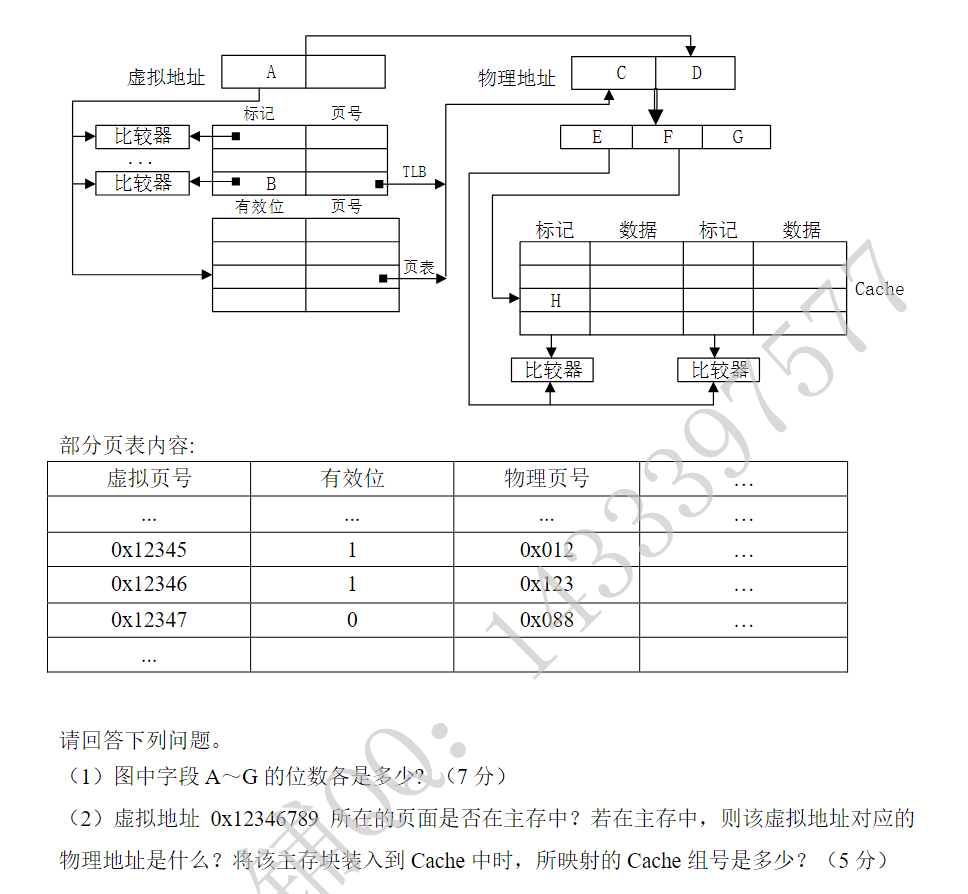
1）A~G位数，B存了什么

页大小 \(8\text KB=2^{13}\),页内偏移地址需要13位（x楼x号门）

A是虚拟页号(x单元楼)，应该用虚拟地址位数减去页内偏移位，即 \(32-13=19\) 位 B是虚拟页号标记位，是和A进行比较的，则应该为 \(19\) 位

物理地址有24位，但是页内偏移需要13位是不能改变的，所以可以得到

C是物理页号，应该用物理地址位数减去页内偏移位，即 \(24-13=11\) 位

D是物理页偏移，就是页内偏移地址，即 \(13\) 位

以上是页表的计算，接下来到了Cache的计算

Cache的数据区有64KB，主存块为 \(64=2^6B\)，那么有 \(64KB/64B=1K=2^{10}\) 块主存

采用2路组相联方式，那么有 \(2^9\) 组

所以组索引应该有9位，块内索引应该有6位，那么物理地址的Cache标记位应该只有 \(24-9-6=9\) 位

E为组内标记位，9位

F为组索引位，9位

G为块内索引，6位

2） 虚拟地址 0x07FFF180 的虚拟页号是 0x07FFF180 >> 13 = 0x03FFF,页内偏移为 0x1180

查一下题目给的页表，0x03FFF 的有效位为 1，所以 该页在主存中，物理页号是 0x153

然后物理地址：0x153<<13+0x1180=0x2A7180 块内偏移取低6位地址，那么我们计算得到块内偏移 \(\mathrm{0x2A7180} \text\& \mathrm{0x3F} =\mathrm{0x00}\)

cache组号取中9位，那么计算得 \((\mathrm{0x2A7180}>>6)\text\&\mathrm{0x1FF}=\mathrm{0x1C6}\)

cache标记位取高9位,即H字段，计算得 \(\mathrm{0x2A7180}>>15=\mathrm{0x54}\)

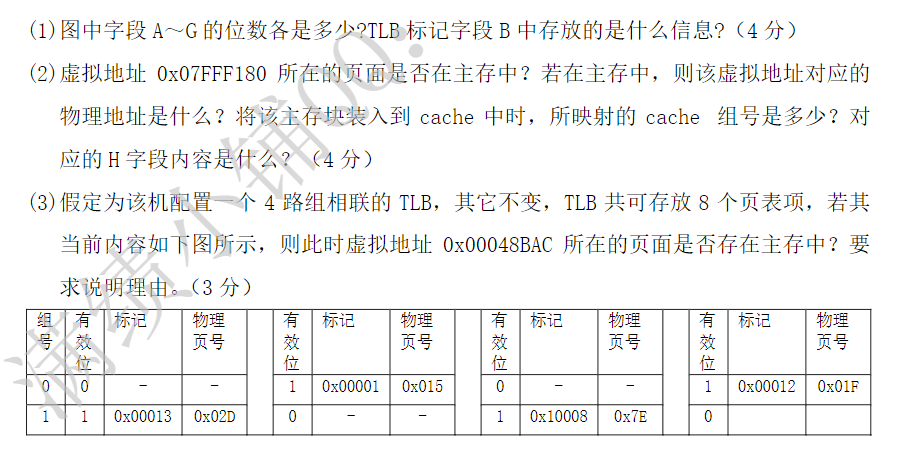
3) 改为4位组相联TLB，且总共8个页表项，那么只有 2 个组，组索引为 1 位， 那么TLB的标记位就是去掉组索引就可以了

虚拟地址 0x00048BAC，挪掉低13位的偏移，得到 \(\mathrm{0x00048BAC}>>13=\mathrm{0x24}\)

所以 \(组号=\mathrm{0x24}\text\& 1=0\)，\(对应标记=\mathrm{0x24}>>1=\mathrm{0x12}\)

查找给出的表，有效位为1，存在于页表中

20-21 WA A

Note

解析 1

\(\dfrac{1}{0.6+0.4/10}=1.5625\)

2\(\dfrac{1.2\times 10^3 \mathrm{MHz}}{0.5\times 2+0.2\times 3+0.1\times 4+0.2\times 5}=400\)

3

无符号：0xFFFD=65533，0xFFDF=65503，0x7FFC=32764

有符号：0xFFFD=-3,0xFFDF=-33,0x7FFC=32764

4

（先改造成RISCV的）对RISC-V指令 bne x10, x21, Exit，当前指令地址为80008（十进制），机器码为0x01551463，问跳转目标地址

bne的开头有b，所以是B型指令，按照指令的拆分进行算一下立即数为imm=+8，得到目标地址为80008+8=80016

5 考察基础知识，把自己想象成汇编程序员，一个个看一下。

指令寄存器是存当前正在执行的指令的，我们在写汇编的时候指令是不被执行的，所以这个应该不可见；

微指令寄存器，加了个微也是指令寄存器，同样不可见；

基址寄存器是参与寻址计算的，我们有时候会静态定义地址偏移，所以这个可见；

标志/状态寄存器，也就是SF、OF这种，我们的条件转移指令是需要依靠这些寄存器的，而条件转移对我们可见，则标志/状态寄存器同样可见

Note

解析 ==6 ==

控制器，没得说

== 7 ==

C：ALU溢出检测，地址对齐/访问检测都是在数据通路里面的

== 8 ==

A：外部中断，这个没什么可解释的

== 9==

这里单周期是900ps，多周期由于addi指令不用做MEM操作，所以应该是200*4=800ps。流水线需要考虑5个操作补全，所以是220*5=1100。

然后单周期是指：一个时钟周期做一个完整的指令，如addi；多周期是指：一个时钟周期做一个完整的阶段操作，如MEM；流水线是指：一个时钟周期尽可能地重叠做阶段操作

Note

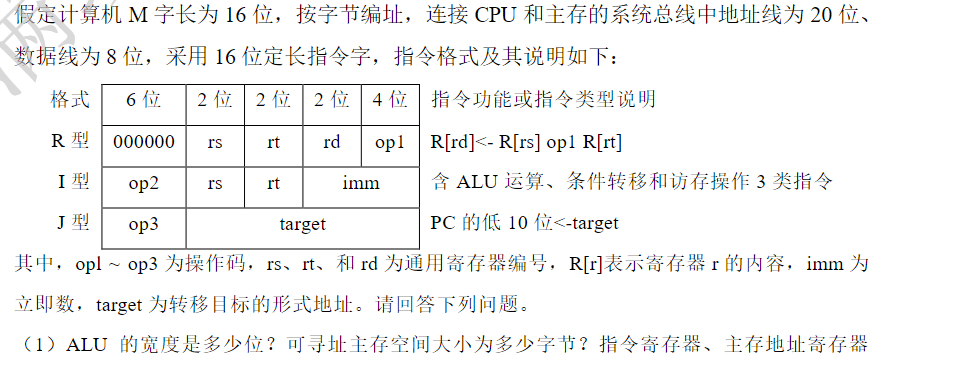
解析 1 ALU和通用寄存器都是按字处理的，计算机M的字长为 16 位，那么ALU的位数也为 16 位

按照字节编址，地址线有 20 位，那么可寻址空间有 \(2^{20}=1\mathrm{MB}\) 指令长度有 16 位，那么指令寄存器有 16 位

MAR的位数和地址线相同，20位 （A=Address）

MDR的位数和数据线相同，8位（D=Data)

2 看表，R型指令的opcode有4位，那么有 \(2^4=16\) 种

I型和J型共用高 6 位，那么有 \(2^6=64\) 种

寄存器段只有 2 位，那么有 \(2^2=4\) 个寄存器

3

01B2H=0000000110110010。高6位000000为R型；rs=01对应R1，rt=10对应R2，rd=11对应R3，op1=0010表示带符号整数减法，所以功能是R3←R1-R2

01B3H仅最后4位变为0011，表示带符号整数乘法，所以功能是R3←R1×R2。

已知R1=B052H，R2=0008H，R3=0020H。

执行01B2H：R3=B052H-0008H=B04AH，符号看作负数减正数仍为负且不发生符号翻转，故不溢出。

随后执行01B3H：R3=R1×R2，R1为带符号值-20398，乘8得-163184，已超出16位带符号范围，发生溢出；

若结果写回按16位截断，则写回值为(-163184)的低16位=8290H。

==4 ==

带符号数要符号扩展

== 5==

J型，即jamp（跳）

I型描述的是条件转移

Note

解析

(1)

\(X=9.625\)，二进制为\(1001.101=1.001101×2^3\)，所以符号位\(S=0\)，阶码\(E=3+127=130=10000010\)，尾数\(M=00110100000000000000000\)，IEEE754单精度为\(\mathrm{0x}411A0000\)。按大端写入从2020H开始的内存：2020H=41，2021H=1A，2022H=00，2023H=00。

Y=-67的32位补码：67的十六进制为\(00000043\text H\)，取反加1得\(FFFFFFBD\text H\)。按大端继续写入：2024H=FF，2025H=FF，2026H=FF，2027H=BD。

(2) 按浮点运算做 \(Z=X+Y\)，先把Y当作浮点数 \(-67.0\) 参与运算。\(X=+1.001101×2^3\)，\(Y=-1.000011×2^6\)。对阶到 \(2^6\)：\(X=+0.001001101×2^6，Y=-1.000011×2^6\)。

符号相反做减法，结果为\(-(1.000011-0.001001101)×2^6=-0.11001011×2^6\)。

规格化：\(-0.11001011×2^6=-1.1001011×2^5\)，对应数值\(-57.375\)。 此时\(S=1\)，\(E=5+127=132=10000100\)，\(M=10010110000000000000000\)， 所以Z的IEEE754单精度十六进制为0xC2658000。

Note

解析

读一个扇区的平均时间=平均寻道时间+平均旋转延迟+数据传输时间。

转速7200RPM=7200/60=120转每秒，所以转一圈时间=1/120秒=0.008333…秒=8.33ms，

平均旋转延迟取半圈=8.33/2=4.17ms。

数据传输率4MB/s，传512B所需时间=512/(4×1024×1024)秒≈0.0001221秒=0.12ms。

总时间≈8.00+4.17+0.12=12.29ms，保留两位小数为12.29ms。

Note

解析

字节编址，块大小4字，每字4字节，那么块内地址要 4 位

Cache存4K字，每块存4字，那么有1K块，块地址需要 10 位

那么标记位需要 32-4-10=18位

再加上有效位1位，脏位(修改位)1位，每块控制位总计20位

\(1K\times 20+4K\times 32=148\) 位（注意这里答案是有问题的，题目问的是按位计算）

Note

解析 (1)

设数据位数m=8，要实现SEC需要校验位数r满足 \(2^r≥m+r+1\)，因为要用r位综合(综合值为0表示无错，1到m+r表示指出哪一位错)。代入m=8，试r=4得 \(2^4=16≥8+4+1=13\) 成立，r=3时 \(2^3=8<12\) 不成立，所以需要4位校验位，总码长n=m+r=12位。

(2)

默认采用偶校验，接收0x945=二进制1001 0100 0101，共12位，按题意编号从MSB到LSB递增，对应位置1到12分别为1 0 0 1 0 1 0 0 0 1 0 1。海明码校验位在位置1、2、4、8，分别检查“位置号二进制中对应位为1”的那些位置(包含该校验位本身)，用异或求偶校验综合：

对p1(位置1)覆盖1,3,5,7,9,11位：1⊕0⊕0⊕0⊕0⊕0=1，说明该组校验不满足，s1=1。

对p2(位置2)覆盖2,3,6,7,10,11位：0⊕0⊕1⊕0⊕1⊕0=0，满足，s2=0。

对p4(位置4)覆盖4,5,6,7,12位：1⊕0⊕1⊕0⊕1=1，不满足，s4=1。

对p8(位置8)覆盖8,9,10,11,12位：0⊕0⊕1⊕0⊕1=0，满足，s8=0。

综合s=s8s4s2s1=0101(二进制)=5，表示第5位出错，把第5位从0翻转为1，得到更正后的码字为1001 1100 0101=0x9C5。

取数据位(非1,2,4,8位)，按位置从小到大即3,5,6,7,9,10,11,12位依次为0 1 1 0 0 1 0 1，得到8位数据01100101=0x65。

Tip

海明码

笔记里没有这个，在这里做一下补充 先说它解决什么问题。海明码的目标是：在传输过程中如果只有 1 位出错，不仅能发现“错了”，还能准确知道“哪一位错了”，并把它改回来。这叫单错纠正，也就是常说的 SEC。 简单来说，不用一个校验位去管所有数据，而是用多个校验位，每个校验位负责“盯住”一部分比特。只要哪几组校验出了问题，就能唯一定位出错的位置。

第一步，先插“检查员”

• 假设你有 8 位数据，不是直接发出去，而是要插入若干校验位。校验位放在特殊的位置：编号是 1、2、4、8、16 这种 2 的幂的位置，其余位置才放数据。
• 比如 8 位数据需要 4 个校验位，总共 12 位，那么第1、2、4、8位是校验位，第3、5、6、7、9、10、11、12位是数据位
• 你可以把校验位想成“检查员”，每个检查员站在一个固定编号的位置上。

第二步，每个校验位负责检查谁

• 规则非常机械：
• 把所有位编号写成二进制
• 某个校验位只检查“编号的某一位是 1”的那些位置
• 举个例子：
• 1号校验位看编号二进制最低位是1的所有位置
• 2号校验位看编号二进制第二位是1的位置
• 4号校验位看第三位是1的位置
• 8号校验位看第四位是1的位置
• 理解成模或许会更明白（？
• 它们各自把自己负责的那些位全部加起来，做“偶校验”（或者奇校验，看题目规定），然后设置自己的值，让总数满足规则。

第三步，接收时怎么判断有没有错

• 接收端什么都不用猜，重新做一遍刚才的检查
• 如果所有校验位检查结果都“对”，那就说明没错。
• 如果有校验位检查不通过，就把这些“出问题的校验位编号”记下来。
• 关键点：把出问题的校验位编号按二进制拼起来，得到的那个数，就是出错的位置编号。
• 比如：1号和4号校验位错了，二进制是 0101，十进制是 5，说明第5位出错

第四步，纠错

• 既然已经知道“第5位错了”，那只要把第5位 0 变 1，或者 1 变 0，就修好了。不需要重传，也不需要额外信息。

先改成RISCV： 改写后的 RISC-V 指令序列为

loop: add x6, x19, x19
add x6, x6, x6
add x6, x6, x22
lw x5, 0(x6)
bne x5, x21, exit
add x19, x19, x20
jal x0, loop
exit:

Note

解析 不知道怎么讲了，直接看做题思路吧

(1) 第1条写 x6，第2条读 x6，属于第1条与第2条关于 x6 的 RAW 相关。

第2条写 x6，第3条读 x6，属于第2条与第3条关于 x6 的 RAW 相关。

第3条写 x6，第4条以 x6 为基址读内存，属于第3条与第4条关于 x6 的 RAW 相关。

第4条写 x5，第5条读 x5 进行比较，属于第4条与第5条关于 x5 的 RAW 相关。

第6条写 x19，而第1条和第6条之间不存在先后读写冲突，因为第1条在前一轮循环完成写回后，第6条才写 x19，不构成同一条流水线内的 RAW 冒险。

(2)

第5条 bne 指令是否跳转会影响后续取指，产生控制相关。

第7条 jal 为无条件跳转，也会改变 PC，同样产生控制相关。

(3)

在不采用转发的情况下，结果只能在 WB 阶段写回后，下一条指令在 ID 阶段后半拍才能读到，因此每一对紧邻的 RAW 相关至少需要插入 2 条 nop。

第1与第2条之间需插入2条 nop。

第2与第3条之间需插入2条 nop。

第3与第4条之间需插入2条 nop。

第4与第5条之间需插入2条 nop。

这些 nop 均插在前一条指令之后。

(4) 采用 EX/MEM、MEM/WB 转发后，第1、2、3条算术指令之间的相关都可以通过转发完全消除，不需要 nop。

第3条 add 与第4条 lw 之间，x6 可从 EX 阶段转发到 EX 阶段地址计算，也无需 nop。

第4条 lw 与第5条 bne 之间属于典型的 load-use 冒险，lw 的数据直到 MEM 阶段结束才可用，即使转发也无法在下一条指令的 EX 阶段使用，因此仍需在第4条之后插入 1 条 nop 才能消除数据冒险。

(5)

若分支是否为零以及 PC 更新在 MEM 阶段完成，则在 bne 之后，已经进入流水线的 IF、ID、EX 三个阶段的指令都可能错误，需要插入 3 条 nop，位置在第5条之后。

若分支判断与 PC 更新在 EX 阶段完成，则只会错误取到 IF、ID 两级的指令，需要插入 2 条 nop，位置同样在第5条之后。

(6)

若更新 PC 的操作在 EX 阶段完成，则在 jal 之后，IF 和 ID 两级的指令无效，需要阻塞 2 个时钟周期。

若更新 PC 的操作提前到 ID 阶段完成，则只有 IF 阶段取到的一条指令无效，流水线只需阻塞 1 个时钟周期。

Note

解析

计弘题的mini版，看上一张卷子的解析，不做赘述

重点题目的解析

第一章：cpi计算。题目：习题6

Note

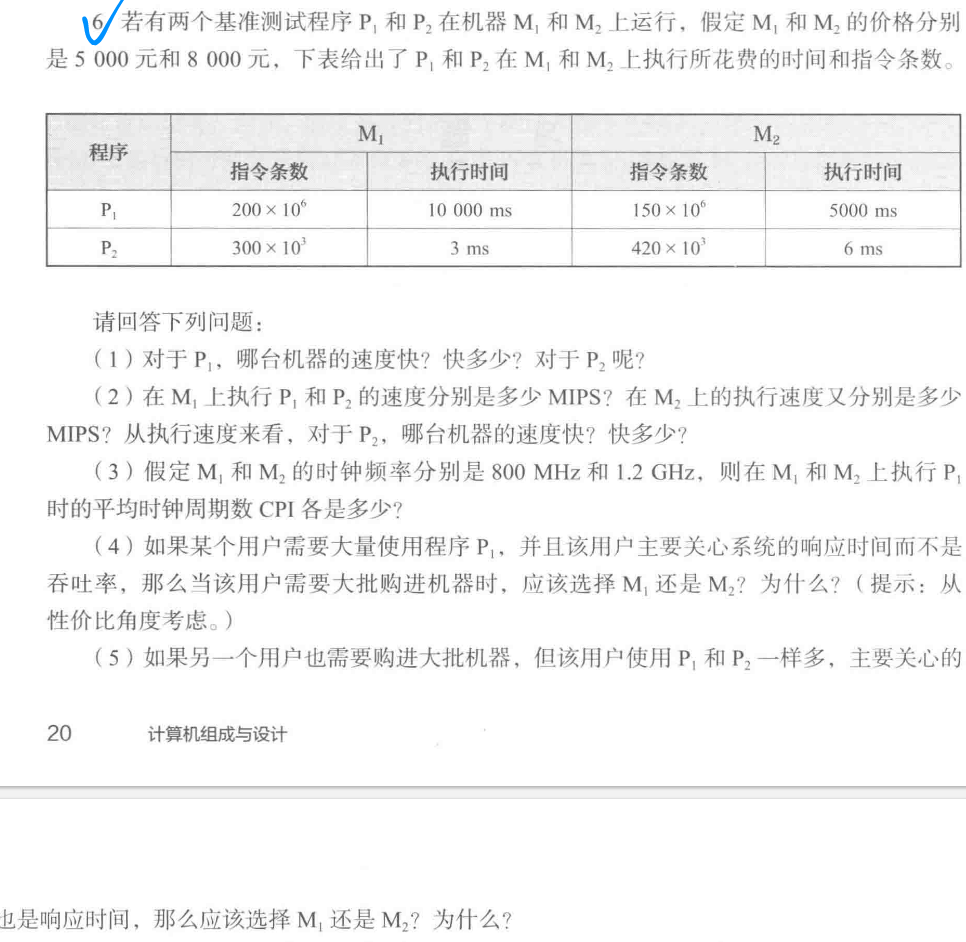
解析 （1）

最能直观反映执行速度的就是执行时间 对\(P_1\)，\(T_{M_1}<T_{M_2}\) 所以M1快，快2倍

对\(P_2\)，\(T_{M_1}>T_{M_2}\) 所以M2快，快2倍

（2） MIPS，即 “指令数 每 秒”，多加一个M（\(10^6\)）单位

对P1：\(\mathrm{MIPS}_{M1}=\dfrac{200\times 10^6}{10000\mathrm{ms}}=20\times 10^6=20\mathrm{MIPS}\)；\(\mathrm{MIPS}_{M2}=\dfrac{150\times 10^6}{5000\mathrm{ms}}=30\mathrm{MIPS}\)

对P2：同理计算得到 100MIPS 和 70MIPS

所以对P1来说，M2快，对P2来说，M1快

（3） CPI，即 “时钟周期 每 指令”

对P1：

\[\begin{align} &\text M1运行P1用时\ &t1=10000ms=10s \\ &\text M1每秒有时钟周期\ &800\text MHZ\ =800\times 10^6 \\ &\text M1运行P1总共用了时钟周期为\ &800\times 10^6(c/s)\times 10s=8\times 10^9 \\ &\text 答案\ &CPI=\dfrac{8\times 10^9}{200\times 10^6}=40 \end{align}\]

其余同理，\(P1_{M_2}=40\)

（4）

从性价比考虑，考虑响应时间，\(M_2=5s,M_1=10s\)

我的做法是 价格/时间，当作性价比

（5）

等概率运行时的期望响应时间（算术平均）

M1： (10 + 0.003)/2 = 5.0015 s

M2： (5 + 0.006)/2 = 2.503 s

M2 平均响应时间更短；再看性能/价格：

M1：(⅕.0015)/5000≈0.19994/5000≈3.999×10^-5

M2：(½.503)/8000≈0.3995/8000≈4.994×10^-5

仍是 M2 更划算，所以应选 M2

第二章：补码、浮点数表示，大小端。题目：题型参考（二、数据表示题）

Note

解析

（1）

先把数写成机器码，再按“小端”放到地址里

\(x=-0.75=-0.11_2=-1.1_2\times 2^{-1}\)

所以 x 的符号位 S=1；阶码 E=-1+127=126；尾数去掉隐藏的1后是\(0.1_2\)。于是得到x的二进制表示

1|011 1111 0|100 0000 0000 0000 0000 0000=0xBF400000

\(i=126=0x007E_{补}\)

按照小端存放如下

地址：40 | 41 | 42 | 43 | 44 | 45
内容：00 | 00 | 40 | BF | 7E | 00

(2)

规格化数的最大值，那么就是阶码取满，尾数取满

阶码取满为（如果全满的话就进入INF了）111 1111 0=254，再减去基数127，得到 127

尾数取满即 23 位的1，也就是 \(2-2^{-23}\)

组合得到 \(2^{127}\times(2-2^{-23})\)(3) short型可以表达的最小值，\(-2^{15}=-32768\)

第三章：补码溢出，浮点数运算舍入。题目：题型参考（三、数据运算题）

Note

解析 0.625规格化：

\(0.625=0.101_2=1.01\times 2^{-1}\)，规格化如下 符号位为0，阶码 \(-1=E-15\Rightarrow E=14=01110_2\), 尾数01... 0|011 10|01 0000 0000

1026规格化： \(1026=100 0000 0010_2=1.00 0000 0010\times 2^10\) 符号位为0，阶码 \(10=E-15\Rightarrow E=25=11001_2\) 0|110 01|00 0000 0010对阶 大指数为10，小指数为-1，指数差为11 将0.625的有效位 1.01 0000 0000 右移11位对齐，超过了目标尾数10位的范围，落入到G/R/S位

尾数相加如下

位置： 尾数 |G|R|S|
1026： 00 0000 0010 |
0.625：00 0000 0000 |1 0 1|

判断舍入** 当前G=1,R=0，S=1，即舍入，尾数+1

00 0000 0011计算答案0|110 01|00 0000 0011=1027

Tip

三位舍入

三位舍入规则里的“三位”，指的是在浮点运算中、目标精度之外 额外保留下来的三个位：Guard 位 G、Round 位 R、Sticky 位 S。它们不属于最终尾数，只用于决定“要不要进 1”。直观定义：在对齐、运算后，你只保留规定的尾数位数（比如半精度是 10 位），紧跟在这 10 位后面的第 1 位叫 Guard 位 G，第 2 位叫 Round 位 R，再往后的所有位只要有一个是 1，就把 Sticky 位 S 记为 1，否则为 0。可以把它理解成：- G 是“第一位被截掉的位”，

• R 是“第二位被截掉的位”，
• S 是“剩下所有被截掉位的或”。

三位舍入配合“就近舍入到偶数（round to nearest even）”的核心判决规则如下。

• 第一种情况，不进位
• 当 G=0 时，说明被截掉的部分小于 0.5 个 ulp（最小有效位单位），直接舍去，尾数保持不变。
• 第二种情况，必进位
• 当 G=1 且 (R=1 或 S=1) 时，说明被截掉的部分严格大于 0.5 ulp，一定要进 1。
• 第三种情况，恰好在 0.5 的“中点”
• 当 G=1，R=0，S=0 时，说明正好是 0.5 ulp 的情况，这时看“当前尾数最低位”：
• 如果尾数最低位是 1，就进 1；
• 如果尾数最低位是 0，就不进。
• 这一步就是“向偶数舍入”，目的是让结果的最低位变成 0，减少长期累计偏差。

简单来说

G=0 不动G=1 且 (R 或 S 为 1) 必进；

G=1 且 R=S=0，看尾数最低位，奇进偶舍。

然后是一些细节 一是进位可能引起尾数全 1 溢出，这时尾数清零，阶码加 1，再判断是否指数溢出。

二是 Sticky 位的作用是“不丢信息”，只要后面任何一位是 1，就能区分“正好一半”和“超过一半”。

第四章：riscv汇编指令含义，c函数汇编。题目：例题4.8，习题19

直接看答案吧，课本有解析

Tip

从本题入手讲解一下常见指令

我们约定reg表示通用寄存器，imm表示立即数（常数）

addi sp, sp. -20：sp保存栈顶，addi是立即数减。这里是栈指针向下挪20字节，是扩容栈的操作

sw reg, imm(sp)：sw即save相关的，将reg里面的东西存到(sp)+imm的地方

lw reg, imm(sp)：lw即load相关的，将(sp)+imm地方的东西存到reg里面

jalr x0, ra, 0：j也就是跳转相关的，x0一般都是0，ra一般表示返回地址(return address)，这里的意思是用ra的地址跳过去，但是不关心返回地址

mv reg1, reg2：这个是 addi的伪指令，将reg2的值传递到reg1中，原本的指令应该为 addi reg1, reg2, 0

li reg, imm：将 立即数 放到 寄存器里

bge reg1, reg2, label：如果reg1的值大于等于reg2的值，跳转到label对应的位置（g：greater 大于；e：equal 等于；l：less 小于）

slli reg1, reg2, imm：将reg2的值左移imm位，放入reg1

lui reg, imm：将一个20位的立即数放到reg的高20位，低12位全部清零，也就是 \(reg=imm<<12\) （Load Upper Immediate）

auipc reg, imm：和lui差不多，不过会将得到的内容再加PC的值，\(reg=PC+(imm<<12)\) (Add Upper Immediate to PC)

Note

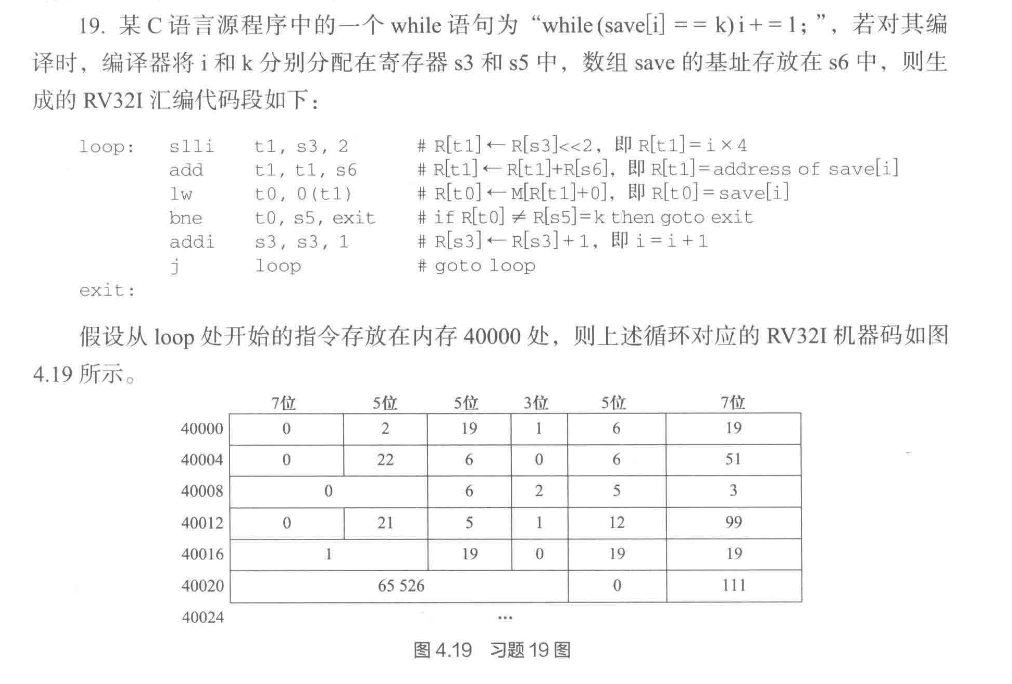
解析 （1）

基本单位是字节

loop: slli t1, s3, 2这里可以看到将 \(i\times 4\) 存入 R[t1]，说明每次的查询save角标是 4i，则save的每个元素占4字节

（2）

左移2位等价于乘4

（3）

R型只涉及reg运算和存取：add、slli

I型一个是imm，一个是reg：lw、addi

B型跳转和条件跳转：bne

J型无条件跳转：j

(4) 对照指令表，可以辨认

一行行看过去

`slli t1, s3, 2` sll为r型，rs2部分为2，rs1和rd分别对应了19和6，那么`s3`就是19，`t1`就是6

> rd一般是存储结果的哪个寄存器，可以靠这个判断

`add t1, t1, s6`，add为r型，这里我们看到rs1和rd都是6，即t1；然后rs2是22，对应`s6`为22

`lw t0,0(t1)`，I型，rd位置为5，说明`t0`为5

`bne t0, s5, exit`，B型，reg1位置是t0，reg2位置就是s5，说明`s5`为1

**==（5）==**

`j loop` 是 jal（jamp and link）的伪指令

操作码 `1101111`，具体编码和跳转目标地址的偏移量有关系

**==（6）==**

我们对表可以看到40012那里的imm为：`0|12`
```c
|imm12|immm10-5|imm4-1|imm11
| 0 | 00000 | 0110 0
```
重组
```c
|0 0 00000 0110 0|（第0位补一个0）=12（offset）
```
exit是跳出循环的条件，对应40012+12=40024

**==（7）==**

J型，依旧超级拼装

65526=1111 1111 1111 0110
```c
|imm20| imm10-1 |imm11|imm19-12
| 1 |111 1111 111 | 1 | 0110
```

重组

```c
|imm20|imm19-12|imm11| imm10-1 |imm0
| 1 | 0110 | 1 |111 1111 111|0
```
即1011 0111 1111 1110，补码转换得到-90001

第五章：流水线冒险、处理，流水线控制信号。题目：题型参考（六、处理器分析题），习题：18，21

Note

解析

add s3, s1, s0 # s3 = s1 + s0
sub t2, s3, s3 # t2 = s3 - s3
lw t1, 0(t2) # t1 = Mem[t2]
add t3, t1, t2 # t3 = t1 + t2
add t1, s4, s5 # t1 = s4 + s5

(1)

简单题简单做

数据转发是：当某些指令使用的寄存器是前面寄存器输出时，数据是否可以直接从前面的执行阶段传递到他需要的指令，而不是从内存或寄存器堆中读取

sub t2, s3, s3用到了 s3 看看它的前面指令有没有 s3 作为输出，发现有的，所以这里需要转发

lw t1, 0(t2) 用到了 t2 看看它的前面指令有没有 t2 作为输出，发现有的，所以这里需要转发

add t3, t1, t2 这里需要 t2 和 t1 的值，前面这俩都是输出，要转发 接下来分析不做赘述

需要转发的寄存器为 s3(I1->I2) t2(I2->I3) t1(I3->I4) t2(I2->I4)

(2)

load-use数据冒险，就看lw指令附近就可以了

lw t1, 0(t2)这里将数据加载到t1；add t3, t1, t2使用了t1，所以load-use数据冒险发生了

Note

解析 分支延迟槽：由于分支条件在**EX阶段** 才能确定，从分支指令进入 IF 阶段到分支结果确定，中间会有：IF->ID->EX。

这就意味着分支指令后面的两条指令已经进入了流水线，所以分支延迟槽为 2 个时钟周期。如果预测错误，这两条指令需要被清空，导致出现了 2 个周期的延迟。

接下来逐步分析数据冒险，由于考虑转发了，所以找 load-use 即可。

lw t0, 0(t1) # 指令4，在MEM阶段才可以得到t0的值
bne t0, s5, Exit # 指令5，在EX阶段需要t0的值判断分支条件

这里lw在MEM阶段才能得到数据，bne在EX阶段就需要数据，所以必须增加一个stall来解决load-use

第六章：cache大小计算，cache、内存页地址划分，cache miss率计算。题目：例题6.8、6.9，习题：15，19

其实这部分最简单，理解了就什么都会了

Note

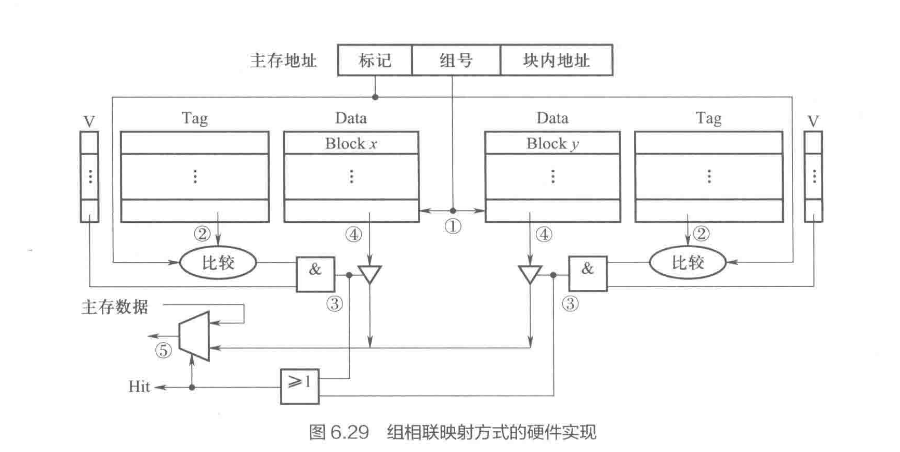
解析

先算一下每一部分要多少位

总位数 \(1MB=2^{20}B\Rightarrow 20位\)

块内地址：\(512B=2^9B\Rightarrow 9 位\)

组号：\(8KB/512B=16块\Rightarrow 8组\Rightarrow 3位\)

标记位：\(20-9-3=8\)

┌────────────┬──────────┬─────────────┐
│ 标记 │ 组号 │ 块内地址 │
│ (Tag) │ (Index) │ (Offset) │
├────────────┼──────────┼─────────────┤
│ 8位 │ 3位 │ 9位 │
│ (19-12) │ (11-9) │ (8-0) │
└────────────┴──────────┴─────────────┘
| ↓ ↓ ↓
| 主存块号 映射组号 块内位置

然后开算

0240CH=0000 0010 0100 0000 1100

地址: 0000 0010 0100 0000 1100
| ┌────────┬────┬──────────┐
| │00000010│010 │000001100 │
| └────────┴────┴──────────┘
| 标记 组号 块内地址

tag：0000 0010

组号：010

块内地址：000001100

所以流程如下

1. 根据地址中间3位找到Cache第2组
2. 将标记位与Cache第2组两个Cache行标记位同时比较
3. 如果有一个相等并且有效位为1，则命中。此时根据低9位的块内地址从对应行中取出单元内容送CPU
4. 若不相等或相等但有效位为0，则为命中，此时将主存的第0000 0010 010块复制到第2组的任意空行，并置有效位为1

Note

解析

Cache 总容量 4096 字；每块 64 字；共 64 块；16 组。

主存总容量 32K 字；每块 64 字；共 512 块。

主存地址需要 \(2^{15}=32K \Rightarrow 15\) 位。块内地址 6 位，组号 4 位，则标记位 5 位。

访问序列 0, 1, 2, ..., 4351，这里会涉及到 \(4351/64=67.98\)，即 68 个块。

4 路组相联映射，则 组号 = 块号 mod 16，块数统计：

组0: 块0, 16, 32, 48, 64 → 5个块
组1: 块1, 17, 33, 49, 65 → 5个块
组2: 块2, 18, 34, 50, 66 → 5个块
组3: 块3, 19, 35, 51, 67 → 5个块
组4: 块4, 20, 36, 52 → 4个块
组5: 块5, 21, 37, 53 → 4个块
...
组15: 块15, 31, 47, 63 → 4个块

对于第一次访问：

0~3 组 5 次访问，填入 5 次块，由于每组最多 4 块，所以会产生 5 次 MISS，即 20 次块 MISS，对应 1280 次字 MISS。

4~15 组 4 次访问，填入 4 次块，每组最多 4 块，所以只有初次填入时会产生 MISS，48 次块 MISS = 3072 次字 MISS。

总计 4352 次字 MISS，全部 MISS，命中率为 0。

对于后九次访问：

0~3 组：每次都会按照 1、2、3、4 的顺序顶掉一个块，刚好全都是需要的，所以总共产生 4×5×9 = 180 次块 MISS。

4~15 组：不存在顶掉情况，全部命中。

总计 180 次块 MISS，即 11520 次字 MISS，总访问次数为 4352×9 = 39168 次，字命中次数为 39168 - 11520 = 27648 次。

总体性能分析：10 次完整访问统计如下

| 访问轮次 | 总访问次数 | Miss次数 | 命中次数 | 命中率 |
| -------- | ---------- | -------- | --------- | ----- |
| 1 | 4352 | 4352 | 0 | 0 |
| 2-10 | 4352 | 1280 | 3072 | 70.59 |
| 总计 | 43520 | 15872 | 27648 | 63.53 |

算性能提升：Cache 命中需要 1 周期，主存访问需要 100 周期。

不用 Cache 的总时间为 4352000 周期。

用 Cache 的总时间为 27648×1 + 15872×101 = 1630720。

提升了 2.67 倍。

Note

解析

(1)

30位主存地址划分:
┌─────────────┬──────────────┬─────────────┐
│ 标记(Tag) │ 块号(Index) │ 偏移(Offset)│
├─────────────┼──────────────┼─────────────┤
│ 14位 │ 9位 │ 7位 │
│ (29-16) │ (15-7) │ (6-0) │
└─────────────┴──────────────┴─────────────┘

(2)

数据区 64KB

标记区：14位×512块=896B

有效位：1位×512块

总计 66496B

Note

解析 (1)

时间局部性是指最近被访问的数据很可能在短时间内再次被访问。

x[i] 和 y[i] 每次都不一样，不具有时间局部性。

空间局部性是指一个存储位置被访问，附近的位置很有可能被访问。

x[i] 和 y[i] 连续存放，空间局部性很强。

命中率推断：高。

(2)

Cache： - 数据区容量: 32 B - 主存块大小: 16 B - Cache 块数: 32 B ÷ 16 B = 2 块

数据类型： - 数组 x: 8 个 float = 32 字节，存放在地址 0000 0040H 开始 - 数组 y: 8 个 float = 32 字节，紧跟在 x 后

主存块划分（块大小 16B）

数组 x (从 0x40 开始): - 块A: 0x00000040 - 0x0000004F (x[0]~x[3]) - 块B: 0x00000050 - 0x0000005F (x[4]~x[7]) 数组 y (从 0x60 开始): - 块C: 0x00000060 - 0x0000006F (y[0]~y[3]) - 块D: 0x00000070 - 0x0000007F (y[4]~y[7])

Cache 块号计算

直接映射：Cache 块号 = (地址 ÷ 块大小) mod Cache 块数

块号计算:

块A: 地址0x40, 块号 = (0x40 ÷ 16) mod 2 = 4 mod 2 = 0
块B: 地址0x50, 块号 = (0x50 ÷ 16) mod 2 = 5 mod 2 = 1
块C: 地址0x60, 块号 = (0x60 ÷ 16) mod 2 = 6 mod 2 = 0
块D: 地址0x70, 块号 = (0x70 ÷ 16) mod 2 = 7 mod 2 = 1

映射关系:

Cache块0 ← 主存块A(x[0]~x[3]), 主存块C(y[0]~y[3])
Cache块1 ← 主存块B(x[4]~x[7]), 主存块D(y[4]~y[7])

循环执行过程:

| 迭代 | 访问 | 地址 | 主存块 | Cache块 | 状态 | 说明 |
|-----|------|------|--------|---------|------|------|
| i=0 | x[0] | 0x40 | A | 0 | Miss | 加载块A |
| i=0 | y[0] | 0x60 | C | 0 | Miss | **替换块A**，加载块C |
| i=1 | x[1] | 0x44 | A | 0 | Miss | **替换块C**，加载块A |
| i=1 | y[1] | 0x64 | C | 0 | Miss | **替换块A**，加载块C |
| i=2 | x[2] | 0x48 | A | 0 | Miss | **替换块C**，加载块A |
| i=2 | y[2] | 0x68 | C | 0 | Miss | **替换块A**，加载块C |
| i=3 | x[3] | 0x4C | A | 0 | Miss | **替换块C**，加载块A |
| i=3 | y[3] | 0x6C | C | 0 | Miss | **替换块A**，加载块C |
| i=4 | x[4] | 0x50 | B | 1 | Miss | 加载块B |
| i=4 | y[4] | 0x70 | D | 1 | Miss | **替换块B**，加载块D |
| i=5 | x[5] | 0x54 | B | 1 | Miss | **替换块D**，加载块B |
| i=5 | y[5] | 0x74 | D | 1 | Miss | **替换块B**，加载块D |
| i=6 | x[6] | 0x58 | B | 1 | Miss | **替换块D**，加载块B |
| i=6 | y[6] | 0x78 | D | 1 | Miss | **替换块B**，加载块D |
| i=7 | x[7] | 0x5C | B | 1 | Miss | **替换块D**，加载块B |
| i=7 | y[7] | 0x7C | D | 1 | Miss | **替换块B**，加载块D |

总访问次数: 16 次 (8 次访问 x + 8 次访问 y)

命中次数: 0 次

Miss 次数: 16 次

命中率: 0%

(3)

块大小 8B，数组占用的块

数组 x (从 0x40 开始，32 字节): - 块0: 0x40-0x47 (x[0], x[1]) - 块1: 0x48-0x4F (x[2], x[3]) - 块2: 0x50-0x57 (x[4], x[5]) - 块3: 0x58-0x5F (x[6], x[7])

数组 y (从 0x60 开始，32 字节): - 块4: 0x60-0x67 (y[0], y[1]) - 块5: 0x68-0x6F (y[2], y[3]) - 块6: 0x70-0x77 (y[4], y[5]) - 块7: 0x78-0x7F (y[6], y[7])

映射公式: 组号 = (地址 ÷ 块大小) mod 组数

块0: 地址0x40, 组号 = (0x40 ÷ 8) mod 2 = 8 mod 2 = 0
块1: 地址0x48, 组号 = (0x48 ÷ 8) mod 2 = 9 mod 2 = 1
块2: 地址0x50, 组号 = (0x50 ÷ 8) mod 2 = 10 mod 2 = 0
块3: 地址0x58, 组号 = (0x58 ÷ 8) mod 2 = 11 mod 2 = 1
块4: 地址0x60, 组号 = (0x60 ÷ 8) mod 2 = 12 mod 2 = 0
块5: 地址0x68, 组号 = (0x68 ÷ 8) mod 2 = 13 mod 2 = 1
块6: 地址0x70, 组号 = (0x70 ÷ 8) mod 2 = 14 mod 2 = 0
块7: 地址0x78, 组号 = (0x78 ÷ 8) mod 2 = 15 mod 2 = 1

映射关系:

组0 (2路): 块0(x[0]~x[1]), 块2(x[4]~x[5]), 块4(y[0]~y[1]), 块6(y[4]~y[5])
组1 (2路): 块1(x[2]~x[3]), 块3(x[6]~x[7]), 块5(y[2]~y[3]), 块7(y[6]~y[7])

访问过程:

| 迭代 | 访问 | 地址 | 主存块 | 组号 | 状态 | 组0状态 | 组1状态 |
|-----|------|------|--------|------|------|---------|---------|
| i=0 | x[0] | 0x40 | 0 | 0 | Miss | [块0, -] | [-, -] |
| i=0 | y[0] | 0x60 | 4 | 0 | Miss | [块0, 块4] | [-, -] |
| i=1 | x[1] | 0x44 | 0 | 0 | **Hit** | [块4, 块0] | [-, -] |
| i=1 | y[1] | 0x64 | 4 | 0 | **Hit** | [块0, 块4] | [-, -] |
| i=2 | x[2] | 0x48 | 1 | 1 | Miss | [块0, 块4] | [块1, -] |
| i=2 | y[2] | 0x68 | 5 | 1 | Miss | [块0, 块4] | [块1, 块5] |
| i=3 | x[3] | 0x4C | 1 | 1 | **Hit** | [块0, 块4] | [块5, 块1] |
| i=3 | y[3] | 0x6C | 5 | 1 | **Hit** | [块0, 块4] | [块1, 块5] |
| i=4 | x[4] | 0x50 | 2 | 0 | Miss | [块4, 块2] | [块1, 块5] |
| i=4 | y[4] | 0x70 | 6 | 0 | Miss | [块2, 块6] | [块1, 块5] |
| i=5 | x[5] | 0x54 | 2 | 0 | **Hit** | [块6, 块2] | [块1, 块5] |
| i=5 | y[5] | 0x74 | 6 | 0 | **Hit** | [块2, 块6] | [块1, 块5] |
| i=6 | x[6] | 0x58 | 3 | 1 | Miss | [块2, 块6] | [块5, 块3] |
| i=6 | y[6] | 0x78 | 7 | 1 | Miss | [块2, 块6] | [块3, 块7] |
| i=7 | x[7] | 0x5C | 3 | 1 | **Hit** | [块2, 块6] | [块7, 块3] |
| i=7 | y[7] | 0x7C | 7 | 1 | **Hit** | [块2, 块6] | [块3, 块7] |

命中率为 50%。

(4)

新的数据布局

数组 x: float[12] = 48 字节

数组 y: float[8] = 32 字节 (不变)

保持问题 (2) 的配置:

• Cache: 32B, 2 块, 每块 16B, 直接映射
• x 从 0x40 开始 地址范围

数组 x (48 字节):

x[0]~x[11]: 0x00000040 ~ 0x0000006F

数组 y (32 字节，紧跟 x 后):

y[0]~y[7]: 0x00000070 ~ 0x0000008F

主存块划分

数组 x 占用的块 (块大小 16B): - 块A: 0x40-0x4F (x[0]~x[3]) - 块B: 0x50-0x5F (x[4]~x[7]) - 块C: 0x60-0x6F (x[8]~x[11]) 数组 y 占用的块: - 块D: 0x70-0x7F (y[0]~y[3]) - 块E: 0x80-0x8F (y[4]~y[7]) Cache 块号映射

块A: (0x40 ÷ 16) mod 2 = 4 mod 2 = 0
块B: (0x50 ÷ 16) mod 2 = 5 mod 2 = 1
块C: (0x60 ÷ 16) mod 2 = 6 mod 2 = 0 ← 与块A冲突!
块D: (0x70 ÷ 16) mod 2 = 7 mod 2 = 1 ← 与块B冲突!
块E: (0x80 ÷ 16) mod 2 = 8 mod 2 = 0 ← 与块A、C冲突!

映射关系:

Cache块0 ← 块A(x[0]~x[3]), 块C(x[8]~x[11]), 块E(y[4]~y[7])
Cache块1 ← 块B(x[4]~x[7]), 块D(y[0]~y[3])

访问序列 (只访问 x[0]~x[7] 和 y[0]~y[7])

注意: 虽然 x 定义为 float[12]，但程序只访问 x[0]~x[7]

| 迭代 | 访问 | 地址 | 主存块 | Cache块 | 状态 | 说明 |
|-----|------|------|--------|---------|------|------|
| i=0 | x[0] | 0x40 | A | 0 | Miss | 加载块A |
| i=0 | y[0] | 0x70 | D | 1 | Miss | 加载块D |
| i=1 | x[1] | 0x44 | A | 0 | **Hit** | 块A在Cache |
| i=1 | y[1] | 0x74 | D | 1 | **Hit** | 块D在Cache |
| i=2 | x[2] | 0x48 | A | 0 | **Hit** | 块A在Cache |
| i=2 | y[2] | 0x78 | D | 1 | **Hit** | 块D在Cache |
| i=3 | x[3] | 0x4C | A | 0 | **Hit** | 块A在Cache |
| i=3 | y[3] | 0x7C | D | 1 | **Hit** | 块D在Cache |
| i=4 | x[4] | 0x50 | B | 1 | Miss | **替换块D**，加载块B |
| i=4 | y[4] | 0x80 | E | 0 | Miss | **替换块A**，加载块E |
| i=5 | x[5] | 0x54 | B | 1 | **Hit** | 块B在Cache |
| i=5 | y[5] | 0x84 | E | 0 | **Hit** | 块E在Cache |
| i=6 | x[6] | 0x58 | B | 1 | **Hit** | 块B在Cache |
| i=6 | y[6] | 0x88 | E | 0 | **Hit** | 块E在Cache |
| i=7 | x[7] | 0x5C | B | 1 | **Hit** | 块B在Cache |
| i=7 | y[7] | 0x8C | E | 0 | **Hit** | 块E在Cache |

命中率计算: 总访问次数 16 次，命中次数 12 次，Miss 次数 4 次，命中率 = 12 / 16 = 75%。