跳转至

RL学习笔记

笔者参看的是周志华老师的《机器学习》，也就是网上很热门的“西瓜书”。笔者必然比不过网上大量的经验，就不做拾人牙慧的事情了，这里主要是记录一些个人的思考，以及完善本书中的一些数学推导（本书中的数学推导确实有些简略了呢，笔者并非数学专业学生，看到公式就头疼）

第一章 绪论

这一部分介绍了一些概念，包括基础术语、假设空间、归纳偏好，然后讲了讲机器学习的发展与历史，比较笼统的串联了一下后面的章节

NFL 定理：对于所有可能的问题和数据分布，任何学习算法的性能都不会在所有问题上普遍优于其他算法。

个人觉得本书这里的后续解释有些混乱，简单来说，NFL 定理证明了：不同的学习算法在不同的问题和数据集上表现不同，无法存在一个“万能的”学习算法，能够在所有任务中表现最佳。

假设样本空间 \(\mathcal{X}\) 和假设空间 \(\mathcal{H}\) 都是离散的，令 \(P\!\left(h \mid X, \Sigma_a\right)\) 代表算法 \(\Sigma_a\) 基于训练数据 \(X\) 产生假设 \(h\) 的概率，再令 \(f\) 代表我们希望学习的真实目标函数。\(\Sigma_a\) 的“训练集外误差”，即 \(\Sigma_a\) 在训练集之外的所有样本上的误差为

\[ E_{ote}(\Sigma_a \mid X, f) = \sum_{h} \sum_{x \in \mathcal{X}-X} P(x)\,\mathbb{I}\!\bigl(h(x) \neq f(x)\bigr)\,P(h \mid X, \Sigma_a) \]

这里做一下解释，这里本质上是一个算期望的过程。

\(E_{ote}(\Sigma_a \mid X, f)\) 表示当测试样本从样本空间中按分布随机抽取、算法输出的假设具有随机性时，算法在测试阶段会犯多大错误的比例

\(\displaystyle\sum_{x \in \mathcal{X}-X}P(x)\) 表示测试样本 \(x\) 是从样本空间 \(\mathcal{X}\) 中按分布 \(P(x)\) 抽取的。也就是说，我们不是只关心某一个特定输入，而是对**所有可能的输入点**按其出现概率加权。

\(\displaystyle \sum_{h\in\mathcal{H}}P(h \mid X, \Sigma_a)\) 表示学习算法 \(\Sigma_a\) 在给定的训练集 \(X\) 的情况下，可能输出不同的假设，并且每个假设 \(h\) 都有一个对应的概率

\(\mathbb{I}\!\bigl(h(x) \neq f(x)\bigr)\) 是损失函数，如果假设 \(h\) 在输入 \(x\) 上预测错误，那么记为 1，预测正确则记为 0

接下来将三个部分乘一起，表示：测试点是 x，算法产生假设是 \(h\)，并且在这个点上预测错误的联合贡献

然后对所有可能的 \(f\) 进行求和，可以得到终式与学习算法无关，进而出现了 NFL 定理（这里原书的推导过程不加赘述）

之后就是经典的“机器学习的发展与历史”，不予赘述

第二章 模型评估与选择

模型总有优劣，倘若泛化性能过低，则称之为过拟合。本质原因是学习能力过于强大，把训练样本所包含的不太一般的特性给学会了

通过实验测试来对学习器的泛化误差进行评估，需要一定的测试集。而为了从数据集中分出测试集和训练集。提出了 留出法，交叉验证法 和 自助法 这样的分离方法。

  • 留出法就是把测试集按比例划分
  • 交叉验证法就是将数据集化成 k 个大小相似的互斥子集，每次用 k-1 个子集作为训练集，另一个作为测试集。称为 k 折交叉验证
  • 自助法就是放回随机抽样，重复样本数量次抽样进行学习

学得模型在实际使用中遇到的数据称为 测试数据，模型评估与选择中用于评估测试的数据集称为 验证即

在研究对比不同算法的泛化性能时，我们用测试集上的判别效果来估计模型在实际使用时的泛化能力，而把训练数据另外划分为训练集和验证集

再接下来，我们有了可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是 性能度量

其中，回归任务 (输出具体数值是多少) 最常用的性能度量是“均方误差”

\[ E(f;D)=\int_{x\sim D}(f(x_i)-y_i)^2p(x)\mathrm{d}x \]

而分类任务比较常用的性能度量是 错误率 和 精度

\[ \begin{align} &E(f;D)=\dfrac{1}{m}\displaystyle\sum_{i=1}^{m}\mathbb{I}(f(x_i)\ne y_i) \\ &acc(f;D)=1-E(f;D) \end{align} \]

但是错误率和精度不能满足所有任务需求，于是提出了 查准率（准确率） 和 查全率（召回率）。

查准率意味着有多少数据被判别为错误，查全率意味着所有准确数据有多少被挑选了出来。

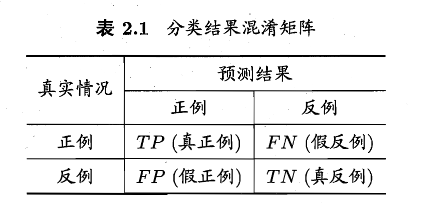
对于二分类问题，可以将样例根据其 真实类别 与 学习器预测类别 的组合划分为真正例 (TP)、假正例 (FP)、真反例 (TN)、假反例 (FN)，如下表，称为分类结果的“混淆矩阵”

image

我们如果根据学习器的预测结果对样例进行排序，排在前面的是 学习器认为最可能是正例的样本，按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、准确率。进而做出“P-R 曲线”，类似下图

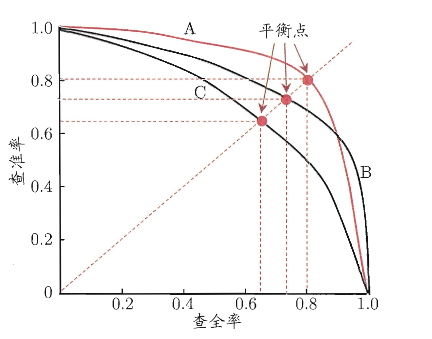
image

如果一个曲线 A 包住了一个曲线 C，那么充分说明学习器 A 优于学习器 C。

但也可以用 BEP(平衡点) 作为一个量度，例如 A 点 BEP=0.8>B 点 BEP，所以可以认为学习器 A 优于学习器 B

BEP 之所以能作为评判学习器优劣的量度，是因为它在不依赖主观阈值的前提下，公平、对称地衡量了模型在查准率与查全率之间的整体平衡能力，特别适用于样本不平衡且错误代价对称的任务。

不过 BEP 还是有些简略了，更常用的是 F1 度量，如下：

\[ F1=\dfrac{2\times P\times R}{P+R}=\dfrac{2\times TP}{样例总数+TP-TN} \]

这里是对准确率和召回率的调和平均数，强烈惩罚了偏科的模型

再然后，我们实际的应用会对查准率 P 和查全率 R 的重视程度有所不同，所以又引入了新的变量，构成了 F1 度量的一般形式 \(F_\beta\)

\[ F_\beta=\dfrac{(1+\beta^2)\times P\times R}{(\beta^2\times P)+R} \]

其实就是把乘法力度设置为了人为的定义

以上是评判模型的泛化能力，也就是评判 模型作为一个分类器是否好用；但我们缺乏一定的量化标准去评判 学习器在不同判别阈值下区分政府样本的整体能力，所以再接下来又提出了 ROC 和 AUC 以作为度量标准

ROC 全称为受试者工作特征，根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别是“真正例率 TPR”和“假正例率 FPR”

\[ \begin{align} TPR=\dfrac{TP}{TP+FN}\\ \\ FPR=\dfrac{FP}{TN+FP} \end{align} \]

可做出类似下面的图

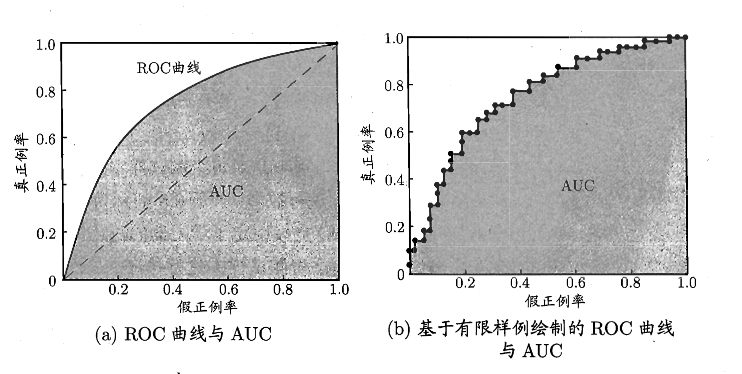
image

然后 AUC(Area Under ROC Curve) 就是 ROC 所包围的面积，用来评判 ROC 的好坏，进而评判学习器的性能

不过现实不是非黑即白的，通常有些预测错误会带来难以想象的代价，所以我们的模型评判要进一步一般化，为错误赋予“非均等代价”

我们可以根据任务的领域知识设定一个“代价矩阵”，如下表，\(cost_{ij}\) 表示将第 \(i\) 类样本预测为第 \(j\) 类样本的代价

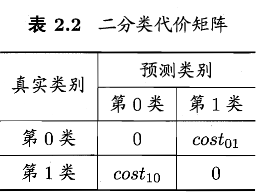
image

一般来说 \(cost_{ij}=0\)，若将第 0 类别为第 1 类所造成的损失更大，则 \(cost_{01}>cost_{10}\)；随时程度相差越大，\(cost_{01}\) 与 \(cost_{10}\) 值的差别越大

于是我们对性能度量扩展其定义，如下

“代价敏感”错误率为

\[ E(f; D; cost) = \frac{1}{m} \left( \sum_{x_i \in D^{+}} \mathbb{I}\!\left(f(x_i) \neq y_i\right)\cdot cost_{01} \;+\; \sum_{x_i \in D^{-}} \mathbb{I}\!\left(f(x_i) \neq y_i\right)\cdot cost_{10} \right) \]

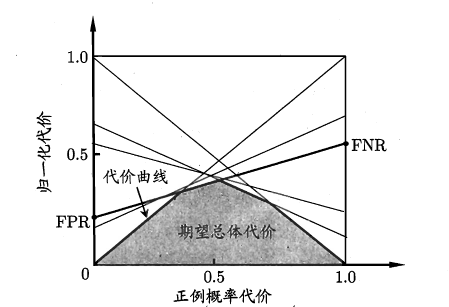
然后再次状态下，ROC 曲线是不可以直接反映出学习器的期望总体代价的，所以又加入了“代价曲线”作为评判。

代价曲线图的横轴是取值为 \([0,1]\) 的正例概率代价如下，其中 \(p\) 是样例为正例的概率：

\[ P(+)_{\text{cost}} = \frac{p \times cost_{01}} {p \times cost_{01} + (1 - p) \times cost_{10}} \]

纵轴是取值为 \([0,1]\) 的归一化代价，如下，其中 FPR 是假正例率，FNR=1-TPR 是假反例率。

\[ cost_{\mathrm{norm}} = \frac{\mathrm{FNR}\times p \times cost_{01} \;+\; \mathrm{FPR}\times (1-p)\times cost_{10}} {p \times cost_{01} + (1-p)\times cost_{10}} \]

接下来我们绘制代价曲线：ROC 曲线上每一点对应代价平面上一条线段，设 ROC 曲线上点的坐标为 \((TPR,FPR)\)，则可以相应地计算出 \(FNR\)，然后在代价平面上做一条从 \((0,FPR)\) 到 \((1,FNR)\) 的线段，线段下的面积即表示了该条件下的期望的总体代价，如下图

image

至此，我们有了完整的实验评估方法和性能度量，但是如今缺少了“比较”的方法。于是提出了 统计假设检验 来对学习器性能比较提供依据。本书以错误率为性能度量，用 \(\epsilon\) 表示

也就是，若在测试集上观察到学习器 A 比 B 好，则 A 的泛化性能是否在统计意义上优于 B，以及这个结论的把握有多大

现实任务中我们并不知道学习器的泛化错误率，只能获知其测试错误率 \(\hat\epsilon\) .泛化错误率与测试错误率未必相同，但直观上，二者接近的可能性应比较大，相差很远的可能性比较小。因此可以根据测试错误率估推处泛化错误率的分布

我们假设 \(m\) 个测试样本，其中泛化错误率为 \(\epsilon\) 的学习器将其中 \(m'\) 个样本误分类、其余样本全都分类正确的概率为 \(\epsilon^{m'}(1-\epsilon)^{m-m'}\)，可以估算处其恰将 \(\hat\epsilon\times m\) 个样本误分类的概率如下

\[ P(\hat{\epsilon}; \epsilon) = \binom{m}{\hat{\epsilon}\times m} \epsilon^{\hat{\epsilon}\times m} (1-\epsilon)^{m-\hat{\epsilon}\times m} \]

给定测试错误率，则解 \(\frac{\partial P(\hat{\epsilon};\epsilon)}{\partial \epsilon} = 0\Rightarrow P(\hat\epsilon ;\epsilon)_{max}\big|_{\epsilon=\hat\epsilon}\)

后面就是一些检验的介绍了

再然后，学习算法除了实验估计其泛化性能，人们往往还希望了解它“为什么”有这样的性能。于是 偏差 - 方差分解 是解释学习算法泛化性能的重要工具

偏差 - 方差分解试图对学习算法的期望泛化错误率进行拆解。算法在不同训练集上学得的结果很可能不同，即便这些训练集是来自同一个分布

我们约定：对一个测试样本 \(\vec x\)，令 \(y_D\) 为 \(\vec x\) 在数据集中的标记，\(y\) 为 \(\vec x\) 的真实标记，\(f(\vec x;D)\) 为训练集 D 上学得模型 \(f\) 在 \(\vec{x}\) 上的预测输出，则

学习算法的期望预测为 \(\bar{f}(x) = \mathbb{E}_{D}\!\left[f(x;D)\right]\)

使用样本数相同的不同训练集产生的方差为 \(\mathrm{var}(x)=\mathbb{E}_{D}\!\left[\left(f(x;D)-\bar{f}(x)\right)^2\right]\)

噪声为 \(\epsilon^2=\mathbb{E}_{D}\!\left[(y_D - y)^2\right]\)

期望输出与真实标记的差别称为偏差 (bias)，即 \(\mathrm{bias}^2(x)=\left(\bar{f}(x)-y\right)^2\)

然后就是一系列数学推导，这里书上的推导相当完善，可以直接看书，最终结论为

\[ E(f;D) = \mathrm{bias}^2(x) + \mathrm{var}(x) + \epsilon^2 \]

即，泛化误差可以分解为偏差、方差和噪声之和

偏差度量了学习算法的期望预测与真是结果的偏离程度，刻画了 学习算法本身的拟合关系

方差度量了同样大小的训练集的变动导致的学习性能的变化，刻画了 数据扰动所造成的影响

噪声则表达了当前任务上学习算法所能达到的期望泛化误差的下届，刻画了 学习问题本身的难度

第三章 线性模型