第九章 聚类
聚类是无监督学习中的一类方法,具体是指:把一堆“没有标签”的数据,按相似性自动分成若干组/簇。同一组/簇里的样本彼此相似,不同组/簇之间的差异更大
性能度量
首先介绍聚类算法涉及的性能度量方案。
聚类性能度量也成为聚类“有效性指标”,用于评估聚类结果的好坏;如果已经明确最终要使用的度量,也可以将其直接作为聚类过程的优化目标
好的聚类直观上应“物以类聚”:簇内相似度高、簇间相似度低。于是可以大致划分出两类性能:
- 外部指标:将聚类结果与某个“参考模型”比较
- 内部指标:不借助参考模型,直接考察聚类结果本身
外部指标:基于样本对的一致/不一致计数
给定数据集 \(D=\{x_1,x_2,\dots,x_m\}\) 假定通过聚类给出的簇划分为 \(\mathcal{C}=\{C_1,C_2,\dots,C_m\}\),而参考模型给出的簇划分为 \(\mathcal{C}^*=\{C_1^*,C_2^*,\dots,C_m^*\}\)。令 \(\lambda\) 表示 \(\mathcal{C}\) 的簇标记向量;\(\lambda^*\) 表示 \(\mathcal{C}^*\) 对应的簇标记向量。
我们将样本两两配对 (仅取 \(i<j\)),可以定义四类样本对集合及其大小:
\[
\begin{align}
&a=|SS|,SS=\{(x_i,x_j)\mid\lambda_i=\lambda_j,\lambda_i^*=\lambda_j^*,i<j\}\tag{9.1}
\\
&b=|SD|,SD=\{(x_i,x_j)\mid\lambda_i=\lambda_j,\lambda_i^*\ne\lambda_j^*,i<j\}\tag{9.2}
\\
&c=|DS|,DS=\{(x_i,x_j)\mid\lambda_i\ne\lambda_j,\lambda_i^*=\lambda_j^*,i<j\}\tag{9.3}
\\
&d=|DD|,DD=\{(x_i,x_j)\mid\lambda_i\ne\lambda_j,\lambda_i^*\ne\lambda_j^*,i<j\}\tag{9.4}
\end{align}
\]
由于每个样本对 \((x_i,x_j)\) 只能落在四类之一,所以有 \(a+b+c+d=\dfrac{m(m-1)}{2}\) 成立
接下来我们根据式(9.1)-(9.4)可以得到常用的外部指标,很好理解
Jaccard系数(JC)
\[
\text{JC}=\dfrac{a}{a+b+c}\tag{9.5}
\]
FM指数
\[
\text{FMI}=\sqrt{
\dfrac{a}{a+b}
\cdot
\dfrac{a}{a+c}
}
\tag{9.6}
\]
Rand指数
\[
\text{RI}=\dfrac{2(a+d)}{m(m-1)}\tag{9.7}
\]
上述外部指标的取值都在 \([0,1]\) ,越大越好
内部指标:基于簇内紧凑与簇间分离
考虑聚类划分 \(\mathcal{C}=\{C_1,C_2,\dots,C_k\}\),我们定义
簇 \(C\) 的簇内平均距离
\[
\text{avg{(C)}}=\dfrac{2}{|C|(|C|-1)}
\sum_{1\le i\le j\le|C|}\text{dist}(x_i,x_j)
\tag{9.8}
\]
\(\text{dist}(\cdot,\cdot)\) 表示两个样本之间的距离
簇 \(C\) 的簇内直径(最大距离)
\[
\text{diam}(C)=\max_{1\le i\le j\le|C|}\text{dist}(x_i,x_j)\tag{9.9}
\]
两簇样本最近样本距离
\[
d_{min}(C_i,C_j)=\min_{x_i\in C_i,x_j\in C_j}\text{dist}(x_i,x_j)\tag{9.10}
\]
两簇中心点距离
\[
d_{cen}(C_i,C_j)=\text{dist}(\mu_i,\mu_j)\tag{9.11}
\]
\(\mu\) 表示簇 \(C\) 的中心点(均值向量)为 \(\mu=\dfrac{1}{|C|}\sum_{1\le i\le|C|}x_i\)
接下来基于式 (9.8)-(9.11),可以得到常用内部指标如下:
DB指数
\[
\begin{equation}
\mathrm{DBI}
=
\frac{1}{k}
\sum_{i=1}^{k}
\max_{j \ne i}
\left(
\frac{
\operatorname{avg}(C_i) + \operatorname{avg}(C_j)
}{
d_{\mathrm{cen}}(\mu_i, \mu_j)
}
\right).
\tag{9.12}
\end{equation}
\]
对每个簇 \(i\),去找一个最糟糕的邻居簇,使得 \(\dfrac{两簇的簇内样本到簇中心平均距离}{两簇中心距离}\) 最大;最后求平均
可见DBI越小,簇内越紧凑、簇间越分离
Dunn指数
\[
\begin{equation}
\mathrm{DI}
=
\min_{1 \le i \le k}
\left\{
\min_{j \ne i}
\left(
\frac{
d_{\min}(C_i, C_j)
}{
\max_{1 \le l \le k} \operatorname{diam}(C_l)
}
\right)
\right\}.
\tag{9.13}
\end{equation}
\]
分子:簇间最小距离,即最近的两簇之间最接近的有多近
分母:最大簇直径,即最松散的簇有多散
接下来再取全局最小,即只要存在一对簇特别近,或存在一个簇特别散,指标就会被拉低。可见DI越大,效果越好
距离计算
刚刚引入了一个函数 \(\text{dist}(\cdot,\cdot)\) 表示两样本之间的距离,但是我们并没有解决这个函数的计算,接下来就是关于这个函数的推导
Note
函数 \(\text{dist}(\cdot,\cdot)\) 应当满足以下基本性质
\[
\begin{align}
&\text{dist}(x_i,x_j)\ge0\tag{9.14非负性}\\
&\text{dist}(x_i,x_j)=0\text{当且仅当}x_i=x_j\tag{9.15同一性}\\
&\text{dist}(x_i,x_j)=\text{dist}(x_j,x_i)\tag{9.16对称性}\\
&\text{dist}(x_i,x_j)\le\text{dist}(x_i,x_k)+\text{dist}(x_k,x_j)\tag{9.17直递性}
\end{align}
\]
给定样本 \(\boldsymbol{x_i}=(x_{i1};x_{i2};\dots;x_{in})\) ,\(\boldsymbol{x_j}=(x_{j1};x_{j2};\dots;x_{jn})\)
比较常用的是 闵可夫斯基距离
\[
\begin{equation}
\mathrm{dist}_{\mathrm{mk}}(x_i, x_j)
=
\left(
\sum_{u=1}^{n}
\left| x_{iu} - x_{ju} \right|^{p}
\right)^{\frac{1}{p}}.
\tag{9.18}
\end{equation}
\]
当 \(p=2\) 时,可以得到 欧氏距离
\[
\begin{equation}
\mathrm{dist}_{\mathrm{ed}}(x_i, x_j)
=
\|x_i - x_j\|_2
=
\sqrt{
\sum_{u=1}^{n}
\left|x_{iu} - x_{ju}\right|^2
}.
\tag{9.19}
\end{equation}
\]
当 \(p=1\) 时,可以得到 曼哈顿距离
\[
\begin{equation}
\mathrm{dist}_{\mathrm{man}}(x_i, x_j)
=
\|x_i - x_j\|_1
=
\sum_{u=1}^{n}
\left|x_{iu} - x_{ju}\right|.
\tag{9.20}
\end{equation}
\]
属性类型与距离
属性又一般分为连续属性和离散属性。前者在定义域上有无穷多个可能的取值,后者在定义域上取值有限。
很明显,连续属性可以简单的计算出距离;
而定义域为{1,2,3}这种的离散属性相对能直接计算属性值的距离,这种属性称为有序属性
但定义域为 \(\{飞机,火车,轮船\}\),不太适合直接计算属性值的距离,这种属性称为无序属性
VDM
明显可知,闵可夫斯基距离只能适用于连续属性和有序属性。那么如何评估无序属性的距离呢,书中介绍了 VDM 方法,如下:
设:
- \(m_{u,a}\) 表示在属性 \(u\) 上取值为 \(a\) 的样本数,
- \(m_{u,a,i}\) 表示在第 \(i\) 个样本簇中在属性 \(u\) 上取值为 \(a\) 的样本数,
- \(k\) 为样本簇数
则属性 \(u\) 上有两个离散值 \(a\) 与 \(b\) 之间的VDM距离为
\[
VDM_p(a,b)=\sum_{i=1}^k\left|\dfrac{m_{u,a,i}}{m_{u,a}}-\dfrac{m_{u,b,i}}{m_{u,b}}\right|^p\tag{9.21}
\]
意味着比较两个取值在各类别中的分布差异
多种距离变种
混合属性距离
于是我们可以将闵可夫斯基距离和VDM结合,处理混合属性。如下假定我们有
- \(n_c\) 个有序属性
- \(n-n_c\) 个无序属性
\[
\text{MinkovDM}_p(x_i,x_j)=
\left(
\sum_{u=1}^{n_c}
\left|
x_{iu}-x_{ju}
\right|^p
+
\sum_{u=1+n_c}^{n}
\text{VDM}_p(x_{iu},x_{ju})
\right)^{\dfrac{1}{p}}
\tag{9.22}
\]
加权距离
当属性的重要性不同的时候,我们可以为每个距离加上一定的权重
\[
\text{dist}_\text{wmk}=(w_1\cdot|x_{i1}-x_{j1}|^p+\dots w_n\cdot|x_{in}-x_{jn}|^p)^\dfrac{1}{p}
\tag{9.23}
\]
距离与相似
一般来说,属性之间距离越大,相似度就越小。但是用于相似度度量的距离未必一定满足距离度量的基本性质,尤其是式(9.17)直递性,如下例子
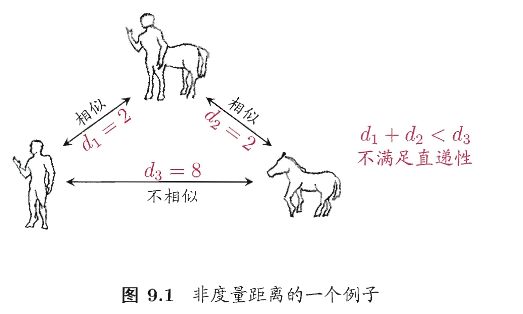
人与人马相似,马与人马相似,但是人与人马完全不相似;这样的距离称为“非度量距离”
此外,本节的距离计算式都是事先定义好的,但是不少的现实任务中,有必要基于数据样本来确定合适的距离计算式,于是有 “距离度量学习” 来实现这一步骤
原型聚类
