第八章 集成学习
集成学习是一种机器学习思想:把多个模型的预测结果进行组合,从而得到比单个模型更稳定、更准确的最终预测
个体与集成
集成学习是通过构建并结合多个个体学习器来完成学习任务,又称“多分类器系统”、“基于委员会的学习”
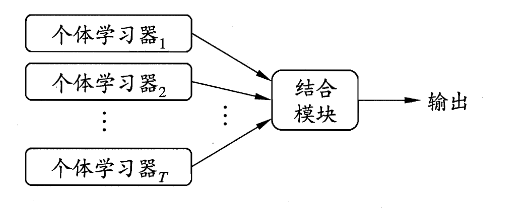
其基本流程为:多个个体学习器 \(\rightarrow\) 结合模块 \(\rightarrow\) 最终输出
个体学习器的类型
同质集成:
- 个体学习器通常由同一种现有的学习算法从训练数据产生,此时集成中只包含同种类型的个体学习器
- 同质集成中的个体学习器也称为“基学习器”,对应算法称为“基学习算法”
异质集成:
- 个体学习器使用不同的学习算法,类型也不同
- 此时个体学习器不称为“基学习器”,而是 组件学习器
好而不同:集成成功的关键条件
准确性:每个个体学习器不能太差;且至少要优于随机猜测
多样性:不同学习器犯错方式不同;且学习器之间存在差异

投票集成的理论分析(二分类)
假设:标签 \(y\in\{-1,+1\}\);每个基分类错误率 \(\epsilon\);错误相互独立
则对每个基分类器 \(h_i\) 有: $$ P(h_i(\boldsymbol{x})\ne f(\boldsymbol{x}))=\epsilon\tag{8.1} $$ 我们假设集成通过简单投票法结合 \(T\) 个基分类器,若有超过半数的基分类器正确,那么集成分类就正确。投票规则如下: $$ H(\boldsymbol{x})=\text{sign}\left(\sum_{i=1}^Th_i(\boldsymbol{x})\right)\tag{8.2} $$ 由一般经验可得,当集成中个体分类数目 \(T\) 增大,集成的错误率将以指数级下降。即 \(T\rightarrow\infty\) 时,错误率趋近于 0
现实情况
刚刚的理论分析中,我们有一个很强的假设:各基学习器错误相互独立;不过由于个体学习器往往在同一数据上训练,错误高度相关。
因此可以得到如下的核心矛盾:提高准确性 和 增加多样性 两者通常互相制约
所以如何产生并结合“好而不同“的个体学习器就是集成学习研究的核心
集成方法的两大类别
根据个体学习器的生成方式,目前的集成学习方法大致可以分为两类,如下
序列化方法:个体学习器之间存在强依赖关系、必须串行生成,代表为 Boosting
并行化方法:个体学习器之间不存在强依赖关系、可同时生成,代表为 Bagging 和 随机森林
Boosting
Boosting是将弱学习器逐步提升为强学习器的集成方法,核心机制如下:
- 现在初始数据分布上训练一个基学习器
- 根据该学习器的错误情况 调整样本分布
- 让后续学习器 更加关注之前分错的样本
- 重复上述过程,直到训练出 \(T\) 个基学习器
- 对所有基学期器进行 加权组合,形成最终模型
所以 Boosting 的学习器生成是序列化的
AdaBoost 的加性模型视角

AdaBoost的最终模型是一个 加性模型 $$ H(\boldsymbol{x})=\sum_{t=1}^T\alpha_th_t(\boldsymbol{x})\tag{8.4} $$ 其中:
- \(h_t(\boldsymbol{x})\in\{-1,+1\}\):第 t 个基分类器
- \(\alpha_t\) 对应权重
而AdaBoost的优化目标是 最小化指数损失函数 $$ \ell_{exp}(H\mid\mathcal{D})=\mathbb{E}_{x\sim\mathcal{D}}\left[e^{-f(\boldsymbol x)H(\boldsymbol x)}\right] \tag{8.5} $$ 其中:
- \(f(\boldsymbol{x})\) 是真实分类函数,\(f(\boldsymbol{x})\in\{-1,+1\}\)
- \(\mathcal{D}\) 为样本分布
指数损失最优解的贝叶斯解释
我们要求最小化指数损失函数,那么很容易想到让式(8.5)对式(8.4)也就是 \(H(\boldsymbol{x})\) 求偏导,如下
再令其为0,解得
进而得到
到这里,式(8.8)证明了 \(\text{sign}(H(\boldsymbol{x}))\) 达到了贝叶斯最优错误率。也就是说,如果指数损失函数最小化,那么分类错误率也将最小(取代了0/1损失函数的位置)
那么,我们可以将此函数作为0/1损失函数的替代,来进行优化,即式(8.5)处提到的AdaBoost优化目标
基学习器权重 \(\alpha_t\) 的推导
AdaBoost中,第一个基分类器 \(h_1\) 通过直接将基学习算法用于初始数据分布得到,此后迭代生成 \(h_t\) 和 \(\alpha_t\)
结合上式(8.4)和(8.8),我们发现,当基分类器 \(h_t\) 基于分布 \(\mathcal{D_t}\) 生成后,该基分类器的权重 \(\alpha_t\) 应该使得 \(\alpha_t h_t\) 最小化指数损失函数
考虑单轮优化:
我们记 \(\epsilon_t= P_{x \sim D_t}\bigl(h_t(x) \ne f(x)\bigr)\)(,可以将上式化为一般式:
这里的 \(\epsilon_t\) 是算法第4行内容,误差率
由于是求权重 \(\alpha_t\),那么将上式对 \(\alpha_t\) 求导:
令(8.10)为零,解得
算法第6行,分类器权重更新公式
样本分布更新的理论来源
经过一次迭代后,整体模型会更新为
于是指数损失也会随之发生变化
由于 \(f^2(x)=h_t^2(x)=1\) ,所以对 \(e^{-f(x)h_t(x)}\) 作泰勒展开近似,如下
AdaBoost中,真实函数与基分类器的输出都被编码为 \(\{-1,+1\}\),因此有 \(f^2(x)=h_t^2(x)=1\)
将这个性质带入到(8.17)也可以进行解释,其中 \(\mathbb{I}(\cdot)\) 为示性函数,内部条件成立时它的输出为1,否则为0
那么可以得到理想的基学习器为
又由于
所以可以得到
即:基学习器在分布 \(\mathcal{D_t}\) 下最小化分类误差
接下来就是更新 \(\mathcal{D_t}\) 和 \(\mathcal{D_{t+1}}\),
在 \(t\) 轮种,我们已经固定 \(H_{t-1}\),要选 \(h\) 让指数损失下降,我们可以把目标整理为
分母中 \(\mathbb{E}_{x \sim \mathcal{D}}\left[e^{-f(x)H_{t-1}(x)}\right]\) 与 x 无关,对 \(\arg\max_h\) 来说只是常数缩放
我们观察(8.14)里乘在 \(f(x)h(x)\) 前面的权重函数
如果原始数据分布记为 \(\mathcal{D}(x)\),那么把它按 \(w_t(x)\) 重新加权,就可以得到一个新的分布,如下
展开来就是
依次类推
算法第7行,样本分布更新公式
分析算法
从偏差-方差分解的角度来看,Boosting主要关注降低偏差,因此可以将泛化能力较弱的学习器提升为强模型
示例
root@iZbp1gtqhrbrar9e0rt59yZ:~/rl/8# python3 2.py
===== 数据集 =====
i= 0 x=[0.1, 0.2] y=1
i= 1 x=[0.2, 0.1] y=1
i= 2 x=[0.35, 0.8] y=1
i= 3 x=[0.4, 0.7] y=-1
i= 4 x=[0.6, 0.3] y=-1
i= 5 x=[0.7, 0.4] y=-1
i= 6 x=[0.8, 0.9] y=-1
i= 7 x=[0.9, 0.85] y=1
===== AdaBoost 迭代开始 =====
----- Round t=1 -----
D_t: ['0.125000', '0.125000', '0.125000', '0.125000', '0.125000', '0.125000', '0.125000', '0.125000']
选择的基学习器 h_t:
feature=0, threshold=0.375000, polarity=1
h_t(x_i): [1, 1, 1, -1, -1, -1, -1, -1]
加权错误率 epsilon_t = P_{x~D}(h!=y) = 0.125000
alpha_t = 1/2 ln((1-eps)/eps) = 0.972955 (公式8.11)
F_t(x_i) = sum_{k<=t} alpha_k h_k(x_i) (公式8.4)
['0.972955', '0.972955', '0.972955', '-0.972955', '-0.972955', '-0.972955', '-0.972955', '-0.972955']
sign(F_t): [1, 1, 1, -1, -1, -1, -1, -1]
训练集0/1错误率:0.125000
指数损失 l_exp(H|D) = E[exp(-f(x)H(x))] (公式8.5)
均匀经验平均:0.661438
按当前 D_t 加权:0.661438
D_{t+1}(i) = D_t(i) * exp(-alpha_t f(x_i) h_t(x_i)) / Z_t (公式8.19)
未归一化: ['0.047246', '0.047246', '0.047246', '0.047246', '0.047246', '0.047246', '0.047246', '0.330719']
Z_t = sum_i 未归一化 = 0.661438
D_{t+1}: ['0.071429', '0.071429', '0.071429', '0.071429', '0.071429', '0.071429', '0.071429', '0.500000']
----- Round t=2 -----
D_t: ['0.071429', '0.071429', '0.071429', '0.071429', '0.071429', '0.071429', '0.071429', '0.500000']
选择的基学习器 h_t:
feature=0, threshold=0.850000, polarity=-1
h_t(x_i): [-1, -1, -1, -1, -1, -1, -1, 1]
加权错误率 epsilon_t = P_{x~D}(h!=y) = 0.214286
alpha_t = 1/2 ln((1-eps)/eps) = 0.649641 (公式8.11)
F_t(x_i) = sum_{k<=t} alpha_k h_k(x_i) (公式8.4)
['0.323314', '0.323314', '0.323314', '-1.622597', '-1.622597', '-1.622597', '-1.622597', '-0.323314']
sign(F_t): [1, 1, 1, -1, -1, -1, -1, -1]
训练集0/1错误率:0.125000
指数损失 l_exp(H|D) = E[exp(-f(x)H(x))] (公式8.5)
均匀经验平均:0.542810
按当前 D_t 加权:0.902334
D_{t+1}(i) = D_t(i) * exp(-alpha_t f(x_i) h_t(x_i)) / Z_t (公式8.19)
未归一化: ['0.136775', '0.136775', '0.136775', '0.037302', '0.037302', '0.037302', '0.037302', '0.261116']
Z_t = sum_i 未归一化 = 0.820652
D_{t+1}: ['0.166667', '0.166667', '0.166667', '0.045455', '0.045455', '0.045455', '0.045455', '0.318182']
----- Round t=3 -----
D_t: ['0.166667', '0.166667', '0.166667', '0.045455', '0.045455', '0.045455', '0.045455', '0.318182']
选择的基学习器 h_t:
feature=1, threshold=0.875000, polarity=1
h_t(x_i): [1, 1, 1, 1, 1, 1, -1, 1]
加权错误率 epsilon_t = P_{x~D}(h!=y) = 0.136364
alpha_t = 1/2 ln((1-eps)/eps) = 0.922913 (公式8.11)
F_t(x_i) = sum_{k<=t} alpha_k h_k(x_i) (公式8.4)
['1.246227', '1.246227', '1.246227', '-0.699683', '-0.699683', '-0.699683', '-2.545510', '0.599600']
sign(F_t): [1, 1, 1, -1, -1, -1, -1, 1]
训练集0/1错误率:0.000000
指数损失 l_exp(H|D) = E[exp(-f(x)H(x))] (公式8.5)
均匀经验平均:0.372557
按当前 D_t 加权:0.389788
D_{t+1}(i) = D_t(i) * exp(-alpha_t f(x_i) h_t(x_i)) / Z_t (公式8.19)
未归一化: ['0.066227', '0.066227', '0.066227', '0.114391', '0.114391', '0.114391', '0.018062', '0.126433']
Z_t = sum_i 未归一化 = 0.686349
D_{t+1}: ['0.096491', '0.096491', '0.096491', '0.166667', '0.166667', '0.166667', '0.026316', '0.184211']
----- Round t=4 -----
D_t: ['0.096491', '0.096491', '0.096491', '0.166667', '0.166667', '0.166667', '0.026316', '0.184211']
选择的基学习器 h_t:
feature=0, threshold=0.375000, polarity=1
h_t(x_i): [1, 1, 1, -1, -1, -1, -1, -1]
加权错误率 epsilon_t = P_{x~D}(h!=y) = 0.184211
alpha_t = 1/2 ln((1-eps)/eps) = 0.744039 (公式8.11)
F_t(x_i) = sum_{k<=t} alpha_k h_k(x_i) (公式8.4)
['1.990265', '1.990265', '1.990265', '-1.443722', '-1.443722', '-1.443722', '-3.289548', '-0.144439']
sign(F_t): [1, 1, 1, -1, -1, -1, -1, -1]
训练集0/1错误率:0.125000
指数损失 l_exp(H|D) = E[exp(-f(x)H(x))] (公式8.5)
均匀经验平均:0.288848
按当前 D_t 加权:0.371399
D_{t+1}(i) = D_t(i) * exp(-alpha_t f(x_i) h_t(x_i)) / Z_t (公式8.19)
未归一化: ['0.045852', '0.045852', '0.045852', '0.079198', '0.079198', '0.079198', '0.012505', '0.387656']
Z_t = sum_i 未归一化 = 0.775312
D_{t+1}: ['0.059140', '0.059140', '0.059140', '0.102151', '0.102151', '0.102151', '0.016129', '0.500000']
----- Round t=5 -----
D_t: ['0.059140', '0.059140', '0.059140', '0.102151', '0.102151', '0.102151', '0.016129', '0.500000']
选择的基学习器 h_t:
feature=1, threshold=0.750000, polarity=-1
h_t(x_i): [-1, -1, 1, -1, -1, -1, 1, 1]
加权错误率 epsilon_t = P_{x~D}(h!=y) = 0.134409
alpha_t = 1/2 ln((1-eps)/eps) = 0.931264 (公式8.11)
F_t(x_i) = sum_{k<=t} alpha_k h_k(x_i) (公式8.4)
['1.059001', '1.059001', '2.921530', '-2.374986', '-2.374986', '-2.374986', '-2.358284', '0.786826']
sign(F_t): [1, 1, 1, -1, -1, -1, -1, 1]
训练集0/1错误率:0.000000
指数损失 l_exp(H|D) = E[exp(-f(x)H(x))] (公式8.5)
均匀经验平均:0.197047
按当前 D_t 加权:0.301879
D_{t+1}(i) = D_t(i) * exp(-alpha_t f(x_i) h_t(x_i)) / Z_t (公式8.19)
未归一化: ['0.150080', '0.150080', '0.023304', '0.040253', '0.040253', '0.040253', '0.040931', '0.197028']
Z_t = sum_i 未归一化 = 0.682182
D_{t+1}: ['0.220000', '0.220000', '0.034161', '0.059006', '0.059006', '0.059006', '0.060000', '0.288820']
===== 最终强分类器 =====
H(x) = sign( sum_t alpha_t h_t(x) )
t=1: alpha=0.972955, stump=(feature=0, thr=0.375000, pol=1)
t=2: alpha=0.649641, stump=(feature=0, thr=0.850000, pol=-1)
t=3: alpha=0.922913, stump=(feature=1, thr=0.875000, pol=1)
t=4: alpha=0.744039, stump=(feature=0, thr=0.375000, pol=1)
t=5: alpha=0.931264, stump=(feature=1, thr=0.750000, pol=-1)
这里算出来的最终模型如下;各个基分类器属性参考feature,阈值参考thr,大于thr则取pol值,负责取-pol:
然后我们假设样本 \(x=[0.30,0.80]\) 带入计算可以得到
得到 \(F(x)=2.921530>0\Rightarrow H(x)=sign(F(x))=+1\)
Bagging 和 随机森林
刚刚讲了序列化的生成方法,下面讲并行化生成方法
总体思路
为了得到泛化能力更强的集成模型,关键是让多个基学习器尽量“有差异”(降低相关性),但又不能差到学不到东西。
做法是:对训练集进行多次采样,得到多个相互有交叠的训练子集,在每个子集上训练一个基学习器,再把它们组合起来。
Bagging

核心做法基于自助采样法(第2章):
- 对大小为 \(m\) 的训练集做 自助采样,每次从原训练集中“有放回”抽取 \(m\) 次,形成一个采样集
- 重复 \(T\) 次,得到 \(T\) 个采样集,训练 \(T\) 个基学习器
- 集成输出:分类问题采用多数投票;回归问题采用平均
之前证明过,自助采样法的训练集中大约63.2% 的样本会至少出现一次进入采样集,其余36.8%没被抽到。
因为每个基学习器都有一部分没见过的样本,可以用这些样本来做该学习器的验证。把对每个样本“没用它训练过的那些学习器”的预测汇总起来,就可以得到 OOB 预测,进而估计泛化误差(相当于一种“自带的交叉验证”,不需要额外划分验证集
令 \(H^{oob}(x)\) 表示对样本 \(x\) 的包外预测,即仅考虑哪些未使用 \(x\) 训练的基学习器在 \(x\) 上的预测,有
用 Bagging 泛化误差的包外估计为
随机森林RF
Bagging的扩展变体,可以看作:Bagging+决策树+额外的属性随机性
具体来说:对基决策树的每个节点,先从该节点的属性集合中随机选择一个包含 \(k\) 个属性的子集,然后再从这个子集中选择一个最优属性用于划分。
这样的话就通过控制参数 \(k\) 达到控制随机性的目的
虽然引入特征随机性会让单棵树变弱,但是树与树之间的相关性更低,整体集成变得更强,泛化误差往往更低
结合策略
截至目前,我们的基学习器相关的算法学得差不多了,接下来是如何结合的问题。
平均法:用于回归/数值输出
假设有 \(T\) 个基学习器,输出数值为 \(h_i(x)\in\mathbb{R}\)
简单平均:
加权平均:
权重通常从数据中学习,但**权重参数多**、训练数据不足或噪声大时容易过拟合,所以实践里“学权重”不一定比简单平均强。
投票法:用于分类
设类别集合 \(\{c_1,\dots,c_N\}\) 。书里把第 \(i\) 个学习器在样本 \(x\) 上对类别 \(c_j\) 的输出写成 \(h_i^j(x)\)
绝对多数投票:
若某类得票超过总票数的一半时输出该类,否则可以拒绝预测
- 这个“拒绝”机制适合对可靠性要求高的场景
- 若任务必须输出结果、不允许拒绝,则会退化为下面的相对多数
相对多数投票:
也就是哪个类票最多就选哪个;若并列最高就随机选一个
加权投票:
不过要注意:
- 不同学习器输出的“概率/得分”不可直接混用,需要先做概率校准(calibration),常见方法包括 Platt scaling、isotonic regression 等。
- 若学习器类型不同、概率尺度不可比,有时要先把概率转成硬标签再投票。
学习法:堆叠
核心思想就是再训练一个二级学习器/元学习器来做结合。
书中将个体学习器称为初级学习器,用于结合的学习器称为次级学习器或元学习器,算法如下

- 先训练 \(T\) 个初级学习器
- 用它们在样本 \(x_i\) 上的输出组成新特征向量 \(z_i=(h_1(x_i),\dots,h_T(x_i))\),并配上原标签 \(y_i\),得到二级训练集 \(D’=\{(z_i,y_i)\}\)
- 在 \(D’\) 上训练二级学习器 \(h’\),最终得到 \(H(x)=h’(h_1(x),\dots,h_T(x))\)
如过直接用训练初级学习器的同一批数据来生成 \(z_i\) ,二级学习器很容易过拟合。
标准做法一般是采用 交叉验证/留一法:对每个样本,用“没见过它”的初级模型输出作为它的二级特征(out-of-fold 预测),再训练二级学习器。
多样性
集成想要泛化强,个体学习器应“好而不同”:既要各自有一定准确性(好),又要彼此不一致/相关性低(不同)。本节给出一个回归任务下的理论分解,并介绍分类任务中常用的多样性度量与增强手段。
误差-分歧分解
假定有 \(T\) 个个体学习器 \(h_1,\dots,h_T\)。用加权平均得到集成输出 \(H(x)=\dfrac{1}{T}\sum_{i=1}^Tw_ih_i(x)\)。任务是回归:目标函数 \(f:\mathbb{R}^d\rightarrow\mathbb{R}\)
首先定义一下 分歧:
todo