第十章降维与度量学习

降维比较好解释，将高维数据（比较多的特征）映射到低维，同时尽量保留有用的结构。用数学语言描述就是：

降维是在学一个“表示/坐标系” \(z=f(x)\)

度量学习则是通过一定的算法，让该近的更近，该远的更远。比方说原本的距离度量用的是欧氏距离，即 \(d(x,y)=||x-y||_2\) ,而度量学习会学得一个更适合任务的距离，比如 Mahalanobis 距离： \(d_M(x,y)=\sqrt{(x-y)\top M (x-y)}，M\succeq0\)，其中 \(M\) 控制不同特征的不同权重，允许特征之间相关性影响距离

\(k\) 近邻学习

首先介绍一下 \(k\) 近邻学习：\(k\) 近邻(kNN)是一类典型的基于实例的监督学习方法：

给定测试样本，先选一个距离度量（欧氏距离/余弦距离/马氏距离等）
在训练集里找离 \(x\) 最近的 \(k\) 个样本

之前学的很多模型，如线性回归、SVM、神经网络等，都有一个明显的训练阶段，用于训练参数 \(\theta\)

但 kNN 几乎不训练，它的训练阶段基本就是把数据存储起来，所以 kNN 也被称为懒惰学习：训练开销低，预测时开销高

如下图所展示的，不同的 \(k\) 会导致不同的分类

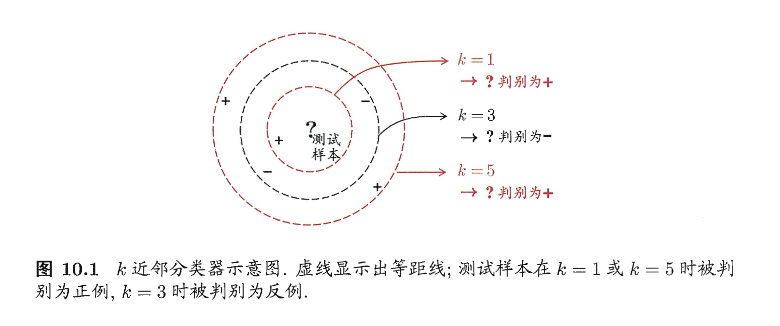
当 k=1 的时候，只看到最近的 1 个点，容易受到噪声的影响，但时边界比较灵活
当 k=3 的时候，看 3 个邻居，多数投票可能反转结果
当 k=5 的时候，更加平滑也更稳定，但是可能抹掉了局部细节

总的来说，kNN的基本过程就是：距离度量 + \(k\) 选择 \(\rightarrow\) 邻居集合 \(\rightarrow\) 投票/平均 \(\rightarrow\) 预测结果

接下来我们理论分析一下 1NN(最近邻分类器) 的泛化错误率如何：

设测试样本为 \(x\) ,其最近邻训练样本为 \(z\) 。当 \(x\) 的真实类别和 \(z\) 的类别不一致的时候，我们给出

\[ P(err)=1-\sum_{c\in\mathcal{Y}}P(c\mid x)P(c\mid z)\tag{10.1} \]

\(\sum_cP(c\mid x)P(c\mid z)\) 表示“x和z在同一类别上的概率一致性”，一致性越大，出错越小

假设样本独立同分布，并且对任意 \(x\) 和任意小的 \(\delta\)，在 \(x\) 附近总能找到训练样本。于是最近邻 \(z\) 会非常接近 \(x\)，那么从概率上就可以近似认为 \(P(c\mid z)\approx P(c\mid x)\)，那么我们把此式带回式(10.1)，可得

\[ P(err)\approx1-\sum_{c\in\mathcal{Y}}P^2(c\mid x) \]

接下来我们令 \(\displaystyle c^*=\arg\max_{c\in\mathcal{Y}}P(c\mid x)\) 来表示贝叶斯最优分类器在 \(x\) 处选择的类别（也就是后验概率最大的类）。然后继续推导上式

\[ \begin{align} P(err)&\approx1-\sum_{c\in\mathcal{Y}}P^2(c\mid x)\\ &\le 1-P^2(c^*\mid x)\\ &=(1+P(c^*\mid x))(1-P(c^*\mid x))\\ &\le2\times(1-P(c^*\mid x))\tag{10.2} \end{align} \]

\(1-P(c^*\mid x)\) 是贝叶斯最优分类器在点 \(x\) 处的错误概率

所以此式意味着：1NN 的泛化错误率不超过贝叶斯最优错误率的 2 倍

第十章降维与度量学习